Logic, before ICs

2020-06-19 electronics design corn dog

So, you want a simple digital logic function in a synthesizer. Maybe it's an AND gate, or a couple of XORs, maybe as much as a shift register. How will you build it?

Today it often makes sense to just throw in a microcontroller chip. They're cheap and versatile. The same microcontroller can be programmed to serve many different purposes, so you can keep just a few types of them in stock, buy them in huge quantities, and that keeps costs down. If you need more speed, then it may make sense to use FPGAs (field-programmable gate arrays), but very few synthesizer circuits really need that much speed.

Twenty or thirty years ago, before microcontrollers were cheap, the usual way of doing a small amount of digital logic was to throw in a couple of MSI (medium-scale integration) logic chips, such as the 7400 or 74LS00 series based on bipolar transistors or the 4000 series based on CMOS. These were small logic building blocks, typically a few gates on each 14-pin or 16-pin DIP chip. There were dozens of popular chips in these series and a few hundred less-common ones. They first existed in the late 1960s but weren't cost-effective and readily available to hobbyists until the mid-1970s. Such chips still exist and you still see a lot of them in DIY designs, but they're gradually falling out of production as cheaper microcontrollers become more appealing to the large commercial interests that are most of the market.

Even further into the past, integrated circuits of any kind were too expensive to be the first choice for hobbyists, and we had to build things out of one active device (transistor or even tube) at a time. I used this kind of logic in my MSK 012 Transistor ADSR. Logic gates built with the minimum number of transistors are barely digital at all: they may be better understood as analog amplifier circuits that happen to be amplifying digital signals. The chips we usually use today, and the gates inside them, have become more complicated and involve more transistors as transistors have become cheaper, but they can be understood as just evolutionary developments from the simplest possible gates.

Here's one of the simplest possible logic gates: a resistor-transistor logic (RTL) inverter. You will sometimes see more complicated circuits, usually with the addition of one or two more resistors to better manage the voltage and current levels, called RTL inverters, but the absolute simplest way to do it is to use just one resistor and one transistor.

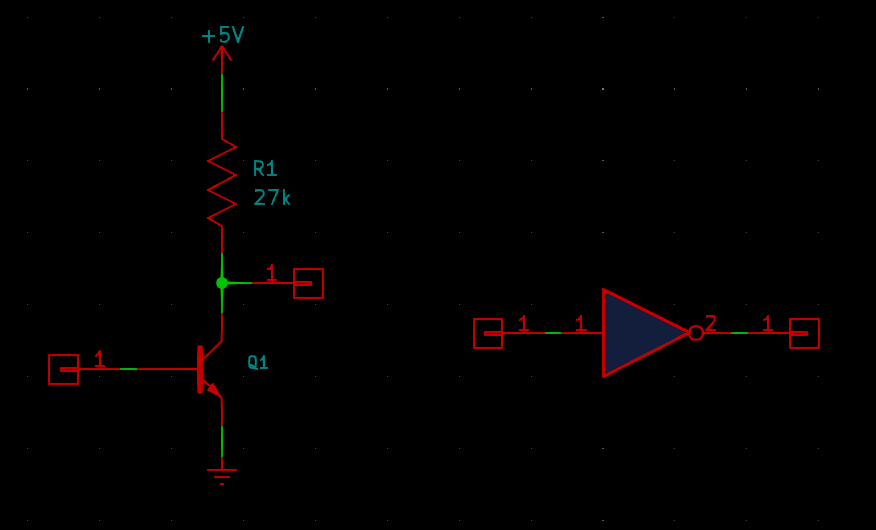
If current flows into the input, the transistor switches on in saturation mode. It pulls the output low - that is, to the transistor's saturation voltage, which might be about 0.2V, with very low impedance. If current doesn't flow into the input, the transistor is switched off, and then the resistor pulls the output high - to the power supply voltage, but with an impedance equal to the resistor value. I've written in 27kΩ but the actual resistance used might vary depending on the application.

This is a rather finicky circuit with several gotchas in how it can be used. The input looks like a diode to ground, so it can't go over about 0.6V without sinking too much current and causing damage to the transistor. The output has low impedance in the low state, but relatively high impedance in the high state. The "high" voltage is not the power supply voltage; it's whatever it floats to given the characteristics of the following input.

It happens that the characteristics of RTL inputs and outputs are just what they need to be to connect to each other. In the high state, the high impedance of the output will allow the actual voltage to drop to just what it needs to be to drive the input transistor of the next gate, while in the low state, the voltage is pulled hard to a low enough voltage to firmly switch off the input transistor. You can connect gates like this one to each other more or less freely. But interfacing simple RTL gates to other things may require a bit more circuitry to make the voltages and currents right. Mixing high impedance in one state and low impedance in the other can have tricky consequences.

Let's look at a more complicated gate. Here's a NAND gate built in a similar minimal style of logic.

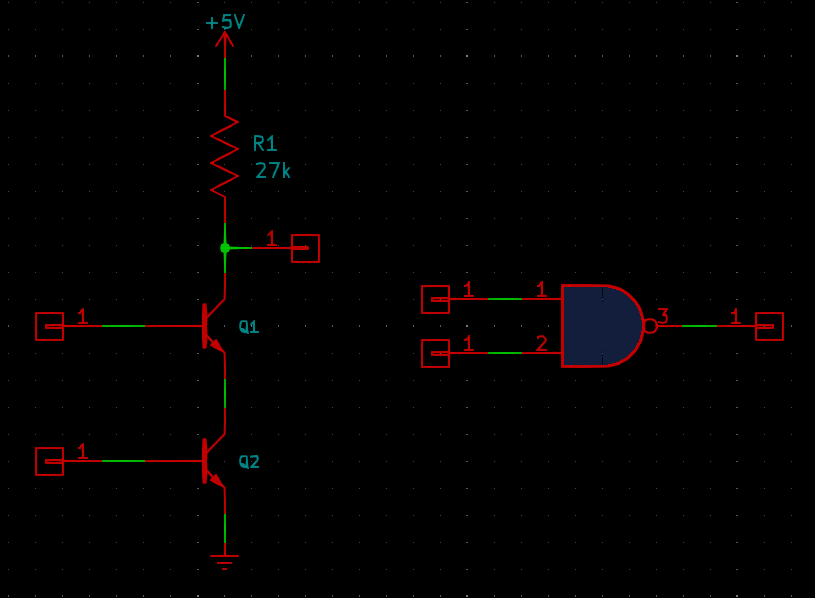
The single transistor has been replaced by two in series. If they both turn on, the output is pulled low. Otherwise, with at least one turned off, no current flows through the pair of them, and the output is high. This gives a two-input NAND logic function.

There are some caveats with this circuit. The output voltage in the low state is going to be twice the saturation voltage of the transistors, and that should be low enough to solidly turn off transistors in subsequent gate inputs. But if extended to more than two inputs with even more transistors in series, this kind of gate might not have a low enough output voltage to work. The need to consider such things is part of the trade-off involved in using a minimalist gate circuit instead of something more complicated that would use additional components to provide less-constrained input and output characteristics.

When there's a series circuit with one function there is often a parallel circuit with a complementary function, and that's the case here. Putting the transistors in parallel instead of in series turns it into a NOR gate.

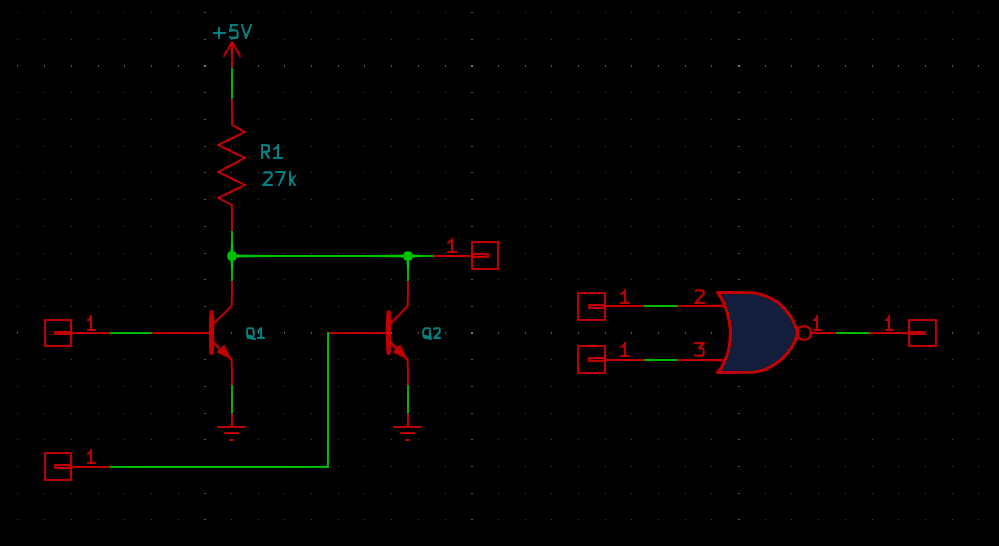
Here, if either or both of the inputs is high, turning on its corresponding transistor, the output is pulled low. Otherwise, when both inputs are low, the resistor pulls the output high. This circuit can be extended to additional inputs with fewer issues than the NAND circuit because the voltages on the transistors do not stack up; with three or four transistors in parallel, the output voltage can still go as low as the saturation voltage of just one of them.

We can build more complicated logic functions out of these smaller blocks. Boolean algebra can rearrange any formula into a combination of a sufficiently large number of NAND gates alone, or NOR gates alone. Sometimes there are also shortcuts available, like this two-transistor XNOR gate. XNOR would otherwise be a difficult logic function to synthesize, requiring a combination of several simpler gates.

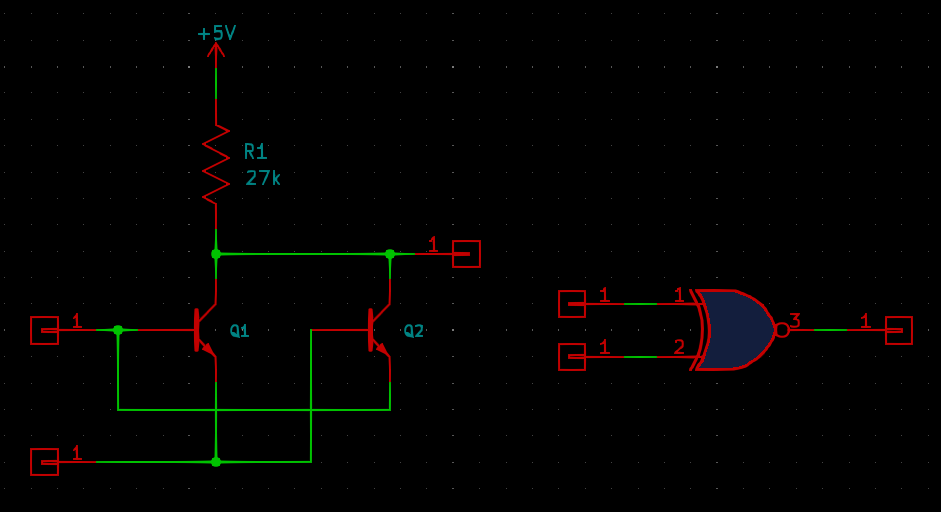
With both inputs high, the output must go high too because there is no other voltage in the circuit. With both inputs low, each transistor sees a low voltage at both its base and emitter, it switches off, and the output is high again. With one input high and the other low, one transistor sees a slightly reverse-biased base-emitter junction but the other switches on, bringing the output low. That makes up the XNOR function. For a XOR gate, just add an inverter on the output; and that might be preferable, to make sure the output characteristics will be well-behaved.

Suppose we connect two inverters in a loop, input to output, with small resistors in between.

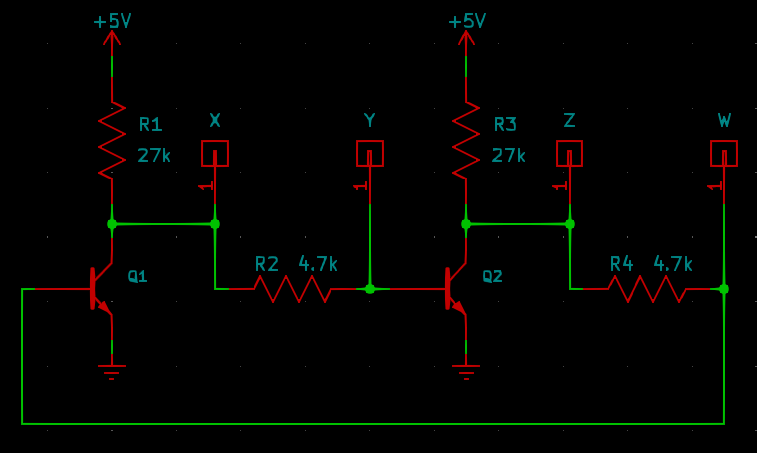
If Q1 is turned on, it brings the points labelled X and Y both low. Then Q2 is turned off, Z and W are both high, and Q1 remains turned on. The circuit is stable in this state. On the other hand, if Q1 is turned off, then X and Y are both high; Q2 will be turned on, Z and W will be low, and that will keep Q1 turned off. This is also a stable state.

This circuit will necessarily settle into one of these two states at power-up. Which one, may be unpredictable, because it may be determined by minute differences in temperature, noise spikes, and so on. But we can force it into a particular state by applying a positive current pulse to one of the inputs, W and Y. That's the reason for the resistors between the stages; the input pulse needs to temporarily override the previous transistor in the loop, and the inter-stage resistors limit the amount of current required to do that.

This circuit is called a bistable multivibrator. It's bistable because it has two stable states; multivibrator will be discussed below. It's a simple digital memory that stores one bit of information, and it's useful in semi-analog kinds of circuits that need to operate in a few different distinct states and switch between them.

If you look up multivibrator circuits on the Web you'll note that they are very often drawn in a specific traditional layout with the wires crossing diagonally in the middle. I'm drawing them differently in this article because I think keeping the direction left-to-right makes it easier to understand how the circuits operate.

Suppose instead of just using resistors between the stages, we put in an RC circuit at one point.

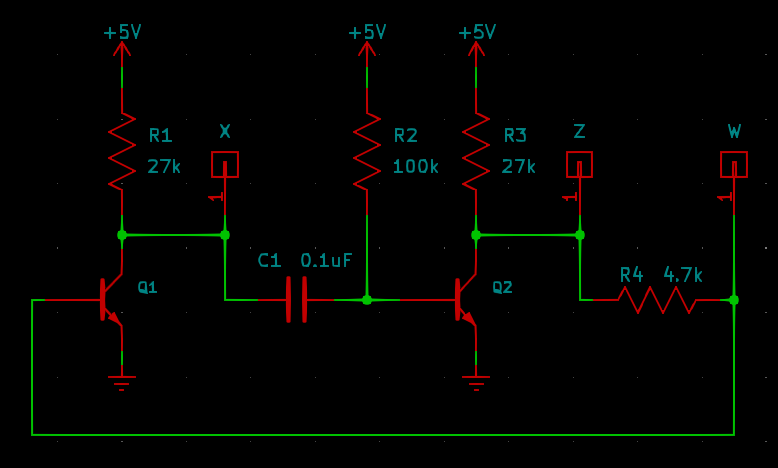
If Q1 is turned off, R1 and R2 are pulling both ends of C1 high, as well as the base of Q2. Then Q2 is turned on, and through R4 it pulls the base of Q1 low, keeping Q1 turned off. The circuit is stable in this state. But what happens if we apply a current pulse to W? Then Q1 briefly turns on. For a short time (while C1 is charging through R2), current flows through C1, pulling the base of Q2 low; that turns off Q2, allowing R3 and R4 to pull the base of Q1 high and keep Q1 turned on even after the external pulse disappears. But it's not stable in this state, because the current through C1 will eventually charge it to the point that Q2's base voltage rises, Q2 turns on, and the circuit returns to its initial state. This circuit is stable in one state, but not the other; it is called a monostable multivibrator, for the one stable state.

The time that the monostable multivibrator can remain in its unstable state is not determined by the initial current pulse, if we can assume that that's very short. Instead it's determined by the charge time of C1 through R2. So this circuit can be used to create a controllable-length pulse or some kind of delay, and that's how it's often used.

Let's replace the second inter-stage resistor with another RC circuit.

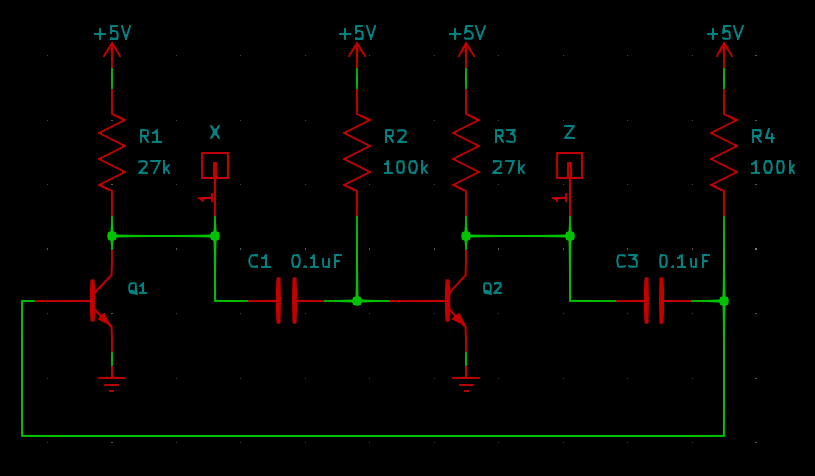
If Q1 is turned on, then for a limited time while C1 charges, it can hold the base of Q2 low, turning off Q2 and allowing the base of Q1 to remain high and keep Q1 turned on. Similarly, if Q2 is turned on, then for a limited time while C3 charges, it holds the base of Q1 low, keeping the base of Q2 high and Q2 turned on. But neither of these states is stable; in each case the capacitor will eventually charge to a voltage that turns on the downstream transistor and switches the circuit to the other state. It keeps toggling back and forth. This circuit is an astable (not stable) multivibrator.

The astable multivibrator is an oscillator producing a rectangle wave: alternating high and low pulses, with the length of the high and low times controlled separately by the pairs C1 and R2, and C3 and R4. This simple two-transistor oscillator used to be a very common way to design an audio oscillator for applications like Morse code practice, in the days before ICs became readily available.

Now, why is it called a multivibrator?

Astable multivibrator circuits were first developed in the early 20th Century, at which time they were built with tubes. In those days, with more complicated kinds of test equipment not yet invented, people often wanted to tune and test radios using marker signals at regular frequency intervals. If you start with a square wave at 10kHz, say, it will have its main harmonics at odd multiples of that: 10kHz, 30kHz, 50kHz, etc. If the square wave has sharp corners, it will include significant energy well into the MHz range. Small amounts of distortion could create smaller spikes at even-multiple frequencies too. If you had a source for such a signal at a precisely known frequency, you could feed it into your receiver and determine the frequencies of other signals by where they stood in relation to the regularly-spaced markers. Calibrating the multivibrator by adjusting it to make one harmonic coincide with a known reference, would also calibrate the frequencies of the other harmonics.

The astable multivibrator circuit was an advance over earlier circuits for this application because it naturally produces square waves. Other oscillators common at the time were usually basically sine oscillators, which would need to be further amplified and clipped to give something resembling square wave output. So the special thing about this circuit was that, unlike the sine oscillators, it could easily produce a spectrum with many frequencies at once: multiple vibrations, hence a multi-vibrator. (Anglicization of the French term multivibrateur in the original paper by Henri Abraham and Eugene Bloch.) Then as the circuit was generalized to also include versions with one or two stable states, people added the words astable, monostable, and bistable to describe different variations on the basic two-element switching circuit.

I've described a few basic logic circuits in minimalist resistor-transistor logic. These circuits, or variations on them, are the kinds of things people used to do simple digital logic in the days before ICs were commonplace. Even though ICs are usually the easiest and cheapest way to do logic today, the basic RTL circuits demonstrate some of the principles still used inside the chips, and they are still relevant in some designs where digital logic is combined with analog circuitry. I've also described multivibrator circuits, which accomplish in a minimum of components the functions for which we might now use timer and flip-flop ICs.

It's been a long time since I posted any corn dogs, so here are some.

◀ PREV Middle Path sample patches || MSK 013 release NEXT ▶

MSK 015 Quad VCA SDIY Kit

US$311.25 including shipping

Comments