Notes on notes on the plane
2017-10-01 music math composition
For this week's Web log entry, I'm digging into my back catalogue again to look at some of the geometry behind the Black Swan Suite. This is all written up in a PDF file with some musical notation and stuff that doesn't work well in HTML; read that if you want details, but I'll give a taste of the construction here.
There's a longstanding idea that the octave is like a circle: if you start at C and start going to higher notes, eventually you wrap around from B to C again, returning where you started. Then it's natural to map notes onto directions on a flat plane.
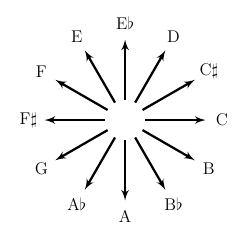
Any process that describes a point moving around on the plane - for instance, the progress of an ant or similar creature wandering around on the plane - generates music. For instance, suppose someone is running around a 30-60-90 triangle:
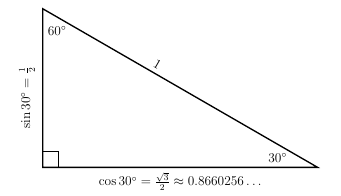
If they go counterclockwise, the note sequence will be F-A-C, arpeggiating an F-major chord; if counterclockise, it'll be B-F#-D#, which arpeggiates a B-major chord. Either way, the timing will be a little weird because of the irrational side lengths. But we could play with the angles to get integer-ratio timings, at the cost of making microtonal music:

For the Black Swan Suite, I took this idea a little further and simulated several characters (Daffy, Elmer, Fanny, Grover, and Hermione) wandering around the geometric plane. Suppose an infinite two-dimensional world is covered with tiles, something like ths:

The four orientations of 30-60-90 triangles here each correspond to two chords. Daffy is not a duck but a black swan. He moves according to a statistical Cauchy flight, which causes him to stay in random locations for short periods, separated by occasional wild leaps to other parts of the plane. This statistical distribution is of interest to people who study things like the stock market that tend to exhibit sudden dramatic changes called black swan events. As Daffy leaps around yelling "hee-hee, whoo-hoo-hoo!" or whatever he does, Elmer and the other characters are hunters, stalking him along the edges of the tiling.
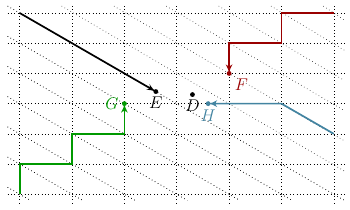
There are a few more rules needed to turn this into music, which are described in the PDF file, but the basic concept is simply that: simulating characters chasing each other around on the plane, with some kind of interesting tiling generating the choices of directions they may move. Each of the hunters corresponds to a voice in the music, with a note generated by each edge along which the character moves, pitch determined by direction and duration determined by length. The complete composition has five movements with a different geometric tiling for each one. Some are 12-EDO; some are microtonal; and the last one in particular uses a very interesting tiling which (in the limit) generates an infinite number of different slopes - so in principle it is ∞-EDO, with no limit on the number of different notes that could be included. I used the Csound software modular synth to generate the actual sounds. It might be an interesting future project to adapt this music for a hardware modular synthesizer.

I will let the music speak for itself at this point. Here's an embedded player for the complete piece (45 minutes); visit the North Coast audio server for shorter tracks corresponding to the individual movements.
◀ PREV Year end || Nucleosynthesis NEXT ▶
