Understanding stabilization capacitors
2017-08-27 design electronics MSK 008 science!
Here's a simplification of the output driver circuit from the MSK 008 Dual VC Octave Switch.
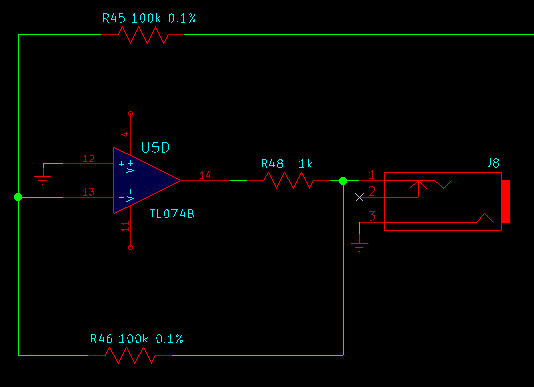
It's a familiar inverting op amp circuit with gain of -1. The op amp's positive input is tied to 0V; it will act to force its negative input to also stay at 0V; and so when the other circuitry not shown to the upper right applies +1V to the input resistor R45, 10µA of current will flow into the "summing node" at the negative input. In order to balance that, the same current must flow through the feedback resistor R46 and bring the tip contact of the output jack to -1V. (The current-limiting resistor R48 can be ignored for the moment; it just forces the op amp to work a little harder.)
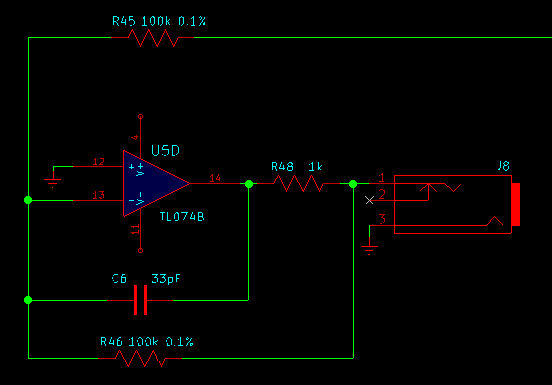
But if you actually look at the MSK 008 schematic in the manual, you'll notice that I've thrown in one more component: a capacitor between pins 13 and 14 of the op amp chip. And it's not unique to this module. Many well-designed op amp circuits include similar capacitors, especially on op amps that drive outputs exposed to the outside world. It's usual to advise beginning designers to include them, but it's much less common for there to be any clear (let alone correct) explanation of why, nor of how to choose their values. I think a lot of people end up just adding capacitors cargo cult style and hoping for the best. This article is meant to make it a little clearer what's really up with these capacitors.
I won't go into a lot of detail on how op amps work internally. That's a subject for another day, and there's some amount of variation among different models of op amp. But in very general terms, there's a differential input stage which detects the difference in voltage between the two inputs, and there's an output stage that can source or sink a fair amount of current. In the TL074B in particular, the input stage is based on JFETs: classic silicon devices that put a reverse-biased diode junction between the input and the rest of the circuit. The reverse-biased junction is effectively an insulator, which gives these devices a very high input impedance. However, it has a certain amount of capacitance, which can slow down the response of the op amp to changes in input voltage. It's also quite hard to match JFETs, which means this kind of op amp in general may have a relatively high input offset voltage because of the mismatch between its two input JFETs. In the MSK 008 I'm using TL074B devices, where the "B" indicates that they're specially selected for low offset. That basically doubles the price of the chip, but it's important for this module, which handles accurate pitch control voltages - and it's a detail many other manufacturers would ignore. Anyway, the important thing to understand for stability is that the op amp detects a small voltage difference on its input, and uses that to switch its current sources and sinks on and off at the output, and the voltage-to-current gain ("transconductance") is large, but not infinite. It also takes more than zero amount of time to respond to any change on the input.
So what happens if there's a sudden change on the input? Let's say a sharp-edged square wave appears on the input side of R45; the voltage there suddenly jumps from +5V to -5V. At DC we'd assume that the op amp negative input is fixed at 0V, but in the very short term, before the op amp can respond through its feedback loop, the voltage on the negative input will go significantly negative. That creates a voltage difference (negative input lower than positive input), so the op amp starts to turn on its current source to bring up the output voltage. It turns on its current source really hard, because there was a lot of voltage difference on the inputs. So the output voltage rises fast, current gets pushed through R46, and that brings the negative input voltage up. When it hits 0V again, the op amp will turn off its current source and we'll be back to normal, where the DC analysis applies and the output voltage is just the negative of the input. All good, right?
But there are time delays involved. When the output reaches +5V, that's where the op amp should stop driving it higher. The information that the output has reached +5V has to make it back through R48 and R46 (which takes a few picoseconds at the speed of light, probably more like a few nanoseconds because of stray reactances in the components), and then it also has to make it through the input delay of the op amp. Remember that those reverse-biased junctions in the JFET front end, although they're nice for DC impedance, mean that the op amp functions as if it had a couple of tiny capacitors built into its inputs. When the output reaches +5V, it still takes a certain amount of time for the feedback current flowing through R46 to charge up the input capacitance of the op amp so that the op amp will turn off its current source. And during that time, the output will have zoomed past +5V. So then the op amp has to correct in the opposite direction, and it can overshoot there as well. It may take several tries to home in on the correct output voltage.
Here's an actual measurement of what the MSK 008 does on square wave input with the stabilization capacitor C6 disabled:
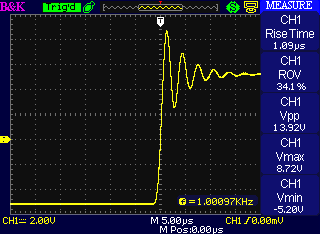
Note the horizontal axis there is not 0V; I had to shift the trace down a bit to fit it all on the screen. Although the target was only +5V, the output overshot all the way to +8.72V, and then there are at least six cycles of back-and-forth, at a rate of a few hundred kHz, before it settles down. (Cautious readers may note this is the response of the entire module, not just the output circuit, but that makes little practical difference to the issues considered here.) This much bounce is pretty bad already, but what would be even worse would be if someone plugged a long patch cable (which has built-in capacitance because of its construction) into the output jack. Then the op amp would be trying to charge the cable's capacitance as well as its own inputs, and the effective delay in its response would be even greater. It's possible that in such a case, the overshoot could be so bad that the back-and-forth hunting process would not damp out, and the amplifier output would just keep bouncing up and down indefinitely: the dreaded parasitic oscillation.
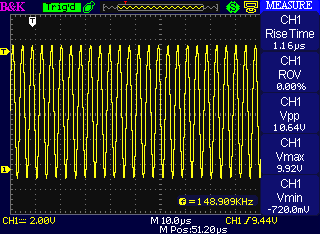
Here's what happens with a standard 1-metre Ad Inifinitum patch cable between the module and the oscilloscope. Remember, the stabilization capacitor is disabled. Real production modules would not do this:
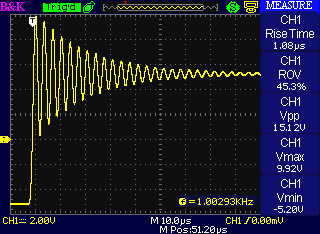
I don't have any cables handy that are long enough to force the module all the way into oscillation, but people might well use cables two or three times longer than mine in a large patch, and I added a 100pF capacitor to the 1-metre cable to simulate that. Generating this much 149kHz on a regular basis without shielding it may screw up marine navigation systems and earn you a visit from the Radio Inspectors:
There are several different techniques for resolving this problem, and even more different mathematical ways to describe them, but one simple way to address it is to say, okay, it's taking too long for the signal to get through the feedback loop; we need to give it a shortcut. Check the schematic again: when the voltage is changing quickly, current from the output can go through C6, bypassing the slower resistive path. When the voltage is changing slowly, C6 (being a very small capacitor) fully charges and looks like an insulator.

This is only a metaphor. In terms of raw latency between one side and the other, the resistive feedback circuit is plenty fast. The time taken for the signal to propagate through the resistors is, as I mentioned, picoseconds to nanoseconds at most, and (from the measurement) we're talking about events on the scale of a few microseconds. So it's not really an issue of the feedback loop not being fast enough. However, the feedback loop (with 101kΩ of resistance in it, let alone some stray inductance) certainly has a limit on how much current it can apply to the inputs of the op amp in those first few moments to counteract any overshoot. The op amp itself is the slow part, and it's made slow by the limited current through the feedback loop. So by adding a small capacitor - which conducts lots of current fast, but only for a short time - we can alter the overall behaviour of the circuit. Another way of thinking about it is that we're adding a certain amount of overshoot to the voltage correction, counteracting the op amp's own tendency to overshoot.
This kind of issue really is significant for all op amps, and without at least a little bit of capacitance in this part of the circuit, the op amp is pretty much guaranteed to oscillate. So why doesn't the op amp have such a capacitor built in? One issue is that capacitors built into integrated circuits are disproportionately expensive. They take up a lot of space on the die. See Zeptobars's die shot of a 741 op amp chip; the compensation capacitor is by far the largest thing on the die, taking up the space of several transistors. The earliest IC op amps did not have integrated stabilization capacitors, and you always had to add one when designing with such chips. Nonetheless, it's so convenient to be able to use an op amp without having to add a stabilization capacitor, that nowadays customers demand it and pretty much all op amps do have them built in, including our TL074B chips. Why, then does it still seem necessary to add an additional, external capacitor?
There's a speed trade-off. If the op amp can't overshoot, it also can't respond extremely fast. The more compensation capacitance we apply, the less the overall circuit is able to respond to high-frequency inputs. The relationship between speed and compensation also depends on the impedance level. We're using a large amount of resistance in the feedback loop for other reasons, which means the op amp's input capacitance charges slower than would be the case with lower-resistance feedback. That and other factors (such as the circuit's gain) mean that the built-in compensation of the TL074B may not be enough here, where it would be enough in some other circuit. Generally, the manufacturers will build the least amount of stabilization capacitance into the chips that they can get away with, and it'll be enough in many applications and will still allow for high-frequency operation, and then in circuits like ours where we need stronger stability and less high-frequency response, we can add our own additional compensation capacitors. It's much easier to add capacitance than to remove it, so it makes sense to have as little as possible built into the chip.
Remember, this is an audio circuit. It doesn't need to work beyond about 100kHz at the absolute most, and really, more like 20kHz. A super-fast op amp would be more a liability than an asset for this module, because of the greater tendency for instability - and that's one reason trying to "upgrade" audio circuits by swapping in op amp chips other than those specified by the designer, can be a bad idea.
Finally, we're faced with the question of how to choose the size of the stabilization capacitor. I think most people really do do this cargo cult style: find out a value that worked once (especially if it was chosen by a designer you respect, but even if that was in some totally different context), and then just use it and hope for the best. A slightly better way to do it would be to think about time constants: given the impedance of the circuit in question as R and the capacitance C, you get a time constant RC which will be on the order of the fastest response time the circuit will allow. If we say the circuit should cover audio, then a response time of 10µs would be reasonable (corresponding to 100kHz) and then with R=100kΩ we'd have a capacitance of 100pF. This is a very approximate calculation, because I haven't defined what I even mean by "response time," and the highest frequency it can reproduce is not necessarily exactly the inverse of the RC time constant, and there is significant relevant capacitance other than what we manually add (for instance, that built into the op amp inputs) and so on. Nonetheless it's a pretty good ballpark estimate.
Accordingly, I built my first prototype of the MSK 008 with 100pF stabilization capacitors. And then I tested it with different frequencies of inputs and found that although it covered all of the audio range (that is, up to 20kHz), it started to attenuate significantly almost immediately after that. Knowing that people imagine they can hear higher frequencies - and are willing to pay for "supertweeters" and such to support that imagination - I don't want someone to feed a 20kHz square wave into the module, scope the output, see that it looks like a sine wave because it only passed the audio part of the signal, and complain. There are also slightly more legitimate reasons to want the module to go a little higher than audio frequencies: for instance, if for some reason you want to use it to process something like a BBD clock.
So I built other prototypes with other capacitances in the loop. I had a lot of 100pF disc capacitors lying around, so I hooked them up in series in twos and threes to give 50pF (which would be 47pF if I used a single standard-value capacitor) and 33pF. Here are the square wave responses with all three values: in order 100pF, 50pF, and 33pF.
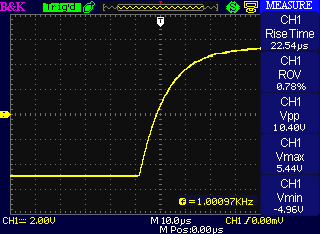
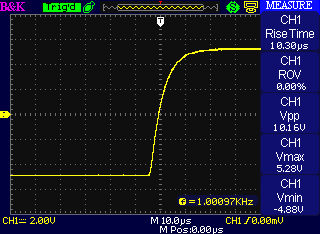
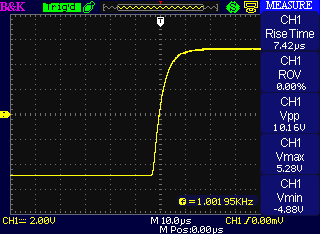
It's clear from the plots that all of them are very well-behaved responses with no overshoot. The rise times as measured by my scope (which I think are measured from 10% to 90% voltage) are pretty much in inverse proportion to the capacitance: 22.5µs for 100pF, half that for 50pF, and a hair over one third for 33pF. At 33pF, with a 7.42µs rise time, you could go up to about 50kHz with a square wave and still see some hint that it wasn't just a sine, and we're still far away from the point where there would be a danger of oscillation. That's the capacitance value I chose for final production use in the MSK 008.
◀ PREV Free EDA software rundown || Video picks NEXT ▶
