What's Euclid got to do with it?
There's a lot of talk in modular synthesis circles about what people call "Euclidean" rhythms, which are claimed to exist in most kinds of traditional music around the world. Unfortunately, this concept is often oversold, and presented in a way that makes it sound much more complicated than it is.
Rounding off a straight rhythm
The simplest kind of rhythm is an isochronous or straight rhythm: just beats repeating at a fixed interval, like a modular clock signal. I generated the audio for this and the other samples in this article by adjusting the feedback on a Leapfrog VCF almost to the point of oscillation and "pinging" it with a Transistor ADSR on the audio input, then mixing that with a burst of red noise from an SSF Quantum Rainbow 2 controlled by a second Transistor ADSR.

That "four on the floor" rhythm feels natural; it's easy to perform and it's used in many kinds of music. It may be the most common musical rhythm in the world. One way to elaborate on it is to subdivide the beats in a binary way. Quarter notes turn into pairs of eighth notes, then into sixteenth notes, and so on. It's usually thought that a more elaborate beat pattern is more "interesting" and easier for the ear to follow.
But instead of cutting beats in half, another thing people sometimes do is play more than one straight beat at once. Suppose we play a 4/4 and a 5/4 straight beat at once, timed so that the measure length is the same for both of them. The top line plays five beats in the same time that the bottom line plays four. Beats coincide at the start of each measure and then shift in and out of sync in a complicated way.
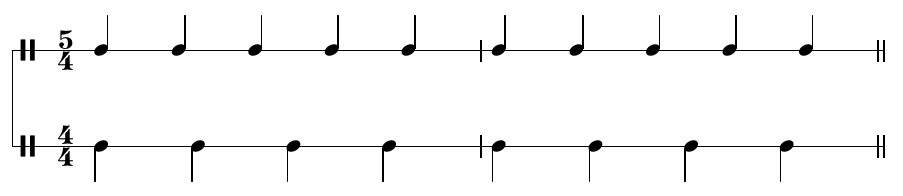
That kind of rhythm, with two straight beats that go in and out of sync, is often claimed to be characteristic of African traditional music. It's difficult to perform. The musicians need a lot of training to do it right, especially if they've already been trained in a system based on binary subdivisions of notes.
Suppose we take the beats of the straight 5/4 rhythm and line them up with the nearest beats of a subdivided 4/4 rhythm. This is the familiar quantization operation of MIDI sequencers. In my example I'm using eighth notes. Be aware that the nearest beat in time is not necessarily the nearest on the page in musical notation because spacing in traditional notation is not directly proportional to time; for my graphics I've overridden LilyPond's normal spacing to make it time-proportional.
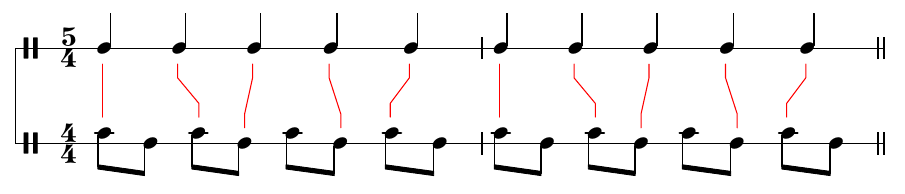
To do it numerically, we can just compute the times as numbers. If we use units of one quarter note of the 4/4 beat, then the beats in the 4/4 beat are at times 0.0, 1.0, 2.0, and 3.0, before starting again at 0.0 for the next measure. One eighth note of this beat is 0.5 time units. The beats of the 5/4 beat happen at intervals of 0.8 time units: 0.0, 0.8, 1.6, 2.4, 3.2. Rounding the numbers for the 5/4 beat off to the nearest eighth notes of the 4/4 beat gives 0.0, 1.0, 1.5, 2.5, 3.0; and those are the times of the eighth notes they match with in my diagram.
If we write down just the eighth-note line that results from quantizing the 5/4 straight rhythm onto eighth notes of a 4/4 straight rhythm, it looks like this.
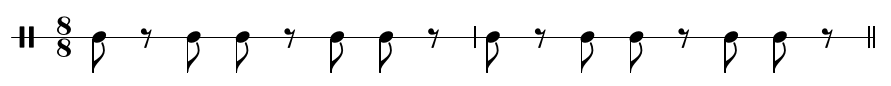
That is the cinquillo rhythm used in Cuban music, and under other names in many other places. It is, exactly, what people call "the Euclidean rhythm" for five notes in eight beats; and that's the best way to understand Eucliden rhythms. They are straight beats quantized onto other straight beats. That's all they are, and quantization is the easiest way to compute them.
Let's call the number of beats that are being quantized k. In this cinquillo example, k=5. Call the number of beats we are quantizing onto n. In my example, n=8. I started out with what I called a 4/4 beat but the quantization is really being done onto an 8/8 beat. Using n<k wouldn't work because we would end up trying to quantize two notes onto the same beat. But in principle we can follow this procedure for any positive integers n and k as long as n is greater than or equal to k.
It's most interesting when n and k are relatively prime, meaning they have no prime factors in common, because common factors between these two numbers cause the result to be a repetition of a simpler rhythm instead of filling the measure. For instance, quantizing a straight 4-beat rhythm onto an 8-beat rhythm just results in the original straight 4-beat rhythm again.
It is an observed fact that the kinds of rhythms you get by doing this, with different numbers of beats in the two straight rhythms you start with, often sound pretty good, and often coincide with rhythms that are already used in traditional music genres. From that observation, some people have attempted to infer that it's some kind of a human universal: that beats formed by quantizing one straight beat onto another naturally sound good and are a fundamental basis for musical perception. Is that true? Hard to say, but there certainly are many traditional beats that do end up being the same as beats that come out of this procedure.
So what DOES Euclid have to do with it?
Discovery of "the" Eucliden rhythm is usually credited to Godfried Toussaint of the School of Computer Science at McGill, with a paper presented at a small workshop in Banff, Alberta, in 2005. You can download an extended version of this paper as a PDF from his Web site.
The best part of the paper is its list of examples of traditional rhythms that can be generated by the quantization procedure; but it starts out by describing a complicated algorithm for calculating the rhythms by rearranging strings of 1s and 0s. Toussaint credits the string-rearrangement algorithm to earlier work by Bjorklund on controlling certain nuclear physics equipment; that algorithm in turn vaguely resembles the well-known Euclidean algorithm for computing the greatest common divisor of two numbers, and that is the reason the name "Euclidean" has become attached to these kinds of rhythms.
I don't think string rearrangement is a good way to compute these rhythmic patterns. Quantization, such as I described above, is easier to implement, and it is more plausible that where the rhythms actually come from psychologically is from something like quantization rather than string rearrangement. I really don't understand why quantization isn't described in Toussaint's paper. He does say that the patterns are "distributed as evenly as possible," which suggests to me that he actually does understand the quantization procedure, but then why present the complicated and opaque string rearrangement instead as the preferred way of calculating them? I note that the paper was presented in an arts workshop, not a computer science or a math conference, and I think the reviewers at those kinds of conferences, or even at a higher-tier arts conference, might have asked for a different emphasis in the algorithmic presentation.
Then the fact that Toussaint says the rhythms can be calculated by Bjorklund's algorithm, and that in turn vaguely resembles a different algorithm attributed to Euclid, is also not a good reason to call the rhythms themselves "Euclidean." But I don't get to decide what people will call things, and since the subject matter is interesting anyway, I'm going to briefly describe Bjorklund's and Euclid's algorithms here.
Suppose we want a rhythm with five notes in an eight-beat framework; k=5, n=8, the same as my earlier example. The result of the calculation will be a string of five 1s representing notes and three 0s representing rests. We start by putting each 1 or 0 into a string of its own. We will rearrange these and merge them until we get them all into a single string with the 1s and 0s spread out as evenly as possible. We start with a list of eight strings, putting the [1] strings first:
[1][1][1][1][1][0][0][0]
There are three odd strings out at the end. We move one of those after each of the first three strings in the list
[1][0][1][0][1][0][1][1]
Then we merge them in, creating three length-two strings.
[10][10][10][1][1]
Now there are two short strings at the end. Again, we move one of them to be after each of the first two strings in the list, and merge.
[101][101][10]
Now, with just one short string left at the end, we stop. The resulting string is 10110110. Translating that into musical notation, this result from Bjorklund's algorithm is the same cinquillo rhythm calculated before.
What about the Euclidean algorithm? For that one, we need some math background. The greatest common divisor or GCD of two positive integers is the largest number that evenly divides both of them. For instance, the divisors of 10 are 1, 2, 5, and 10; the divisors of 12 are 1, 2, 3, 4, 6, and 12; and the GCD of 10 and 12 is the largest number to be found on both those lists, namely 2. A pair of numbers is relatively prime - like 5 and 8 - if and only if their GCD is 1, and those pairs are the pairs that produce the most interesting quantized rhythms.
The Euclidean algorithm, then, is a way of finding out the GCD of two numbers. You start by dividing the larger one by the smaller one and finding the remainder; then you throw out the larger number and repeat the procedure to find the GCD of the smaller number and the remainder you just computed. The last nonzero remainder is the GCD you're looking for.
For instance, starting with 5 and 8: compute 8 divided by 5, it is 1 with remainder 3. Now throw out 8 and use 5 and 3. Compute 5 divided by 3, it is 1 with remainder 2. Compute 3 divided by 2, it is 1 with remainder 1. Then 2 divided by 1 has remainder 0. The last nonzero remainder was 1, so the GCD of 8 and 5 is 1, and that's correct.
As another example with a result that isn't 1: start with 12 and 10. Divide 12 by 10, we get 1 remainder 2. Then 10 divided by 2 is 5 remainder 0. The last nonzero remainder was 2, which again is the correct GCD.
The Euclidean algorithm feels to a computer scientist like it's kind of the same as Bjorklund's algorithm because the steps line up. When computing the n=8, k=5 case, we started with 8 strings, 5 at the start and 3 at the end. Then after shifting and merging, we had 5 strings, 3 at the start and 2 at the end. Then we had 3 strings, 2 at the start and 1 at the end. That pattern of numbers, (8,5,3), (5,3,2), (3,2,1), is the same pattern that showed up when doing the Euclidean algorithm to find out that 1 is the GCD of 8 and 5. After digging through Toussaint's and Bjorklund's papers and some of their references it is possible to make this connection more formal.
And that's why people say cinquillo is a "Euclidean" rhythm.
◀ PREV Design mistakes in synth schematics || Middle Path sample patches NEXT ▶

MSK 008 Dual VC Octave Switch
US$199.83 including shipping
Comments
As for the scale-generation thing: yes, it seems like the same kind of process. Just like with rhythms it's possible to have an endless argument about whether popular scales *come from* the quantization, or quantization just happens to be a property of popular scales. The diatonic scale in particular has many interesting properties and there's no agreement on which ones are important ones that give it its popularity.
There's an idea from Joseph Yasser of a natural evolution from 5-EDO to 7-EDO to 12-EDO with each earlier scale getting quantized into the next, to form an imperfectly uniformly-spaced scale. The next step after 12-EDO would be 19-EDO (Fibonacci sequence...). It's described in chapters 3 and 11 of Joel Mandelbaum's thesis here: http://anaphoria.com/mandelbaum.html I'm not convinced that this is a natural and necessary process - it could easily be cast as a just so story - but it could at least be a fun source of inspiration for new music.