Alternate harmony with additive synthesis
2018-04-22 software music math composition
Much of musical harmony comes down to combining notes that share harmonics. Sounds produced by (some...) physical objects typically have consistent waveforms, where each wave is the same shape as the last. That is also typical of modular-synth oscillators; and its consequence is that the spectrum always consists of a sum of sine waves all at integer multiples called harmonics of one frequency called the fundamental. The proportions and phases of the different harmonics determine the shape of the waves, and those can vary a lot, but the general pattern of integer multiples is fixed. If you play a note like D with a fundamental frequency of 293.7 Hz, it will have its harmonics at 293.7 Hz, 587.4 Hz, 881.1 Hz, 1174.8 Hz, 1468.5 Hz, 1762.2 Hz, and so on.
Now suppose at the same time you play an A with a fundamental frequency of 440.0 Hz. Its harmonics will be at 440.0 Hz, 880.0 Hz, 1320.0 Hz, 1760.0 Hz, and so on. Now, look at those numbers.
D: 293.7, 587.4, 881.1, 1174.8, 1468.5, 1762.2, ...
A: 440.0 Hz, 880.0, 1320.0, 1760.0, ...
Every third harmonic of D is almost exactly the same as every second harmonic of A. When you play these two notes at once, these harmonics reinforce each other, causing the two notes to merge into a single coherent sound; the foundation of a chord. There's no big mystery why this happens: it is because the ratio between the fundamentals (440.0/293.7) is almost exactly a fraction made of two small integers: 3/2. (The reason I keep writing "almost" - these ratios are not exact with the numbers shown - is complicated, but will be discussed below.)
Music as we know it today has evolved rules and practices that make it easy to choose notes which will sound good together. When you choose a standard diatonic scale like say F major (that is: F, G, A, B♭, C, D, E) you get a set of notes that almost all sound good together pairwise (with the exception of the tritone E and B♭) because they have a lot of shared harmonics. Musicologists argue endlessly about how mathematically necessary this system is. Does it sound good because it is some kind of optimum in terms of shared harmonics, and shared harmonics are really important in a way that goes beyond human assumptions? Or is just that we have trained ourselves to expect to hear the diatonic scale?
Well, without answering that question, here's something we could do that might be interesting. Using computer techniques we can create sounds in which the "harmonics" (properly called the partials in this case) are not integer multiples of the fundamental. We'll put them in some other kind of pattern. And then we'll also warp the scale so that we still have notes that share partials in the same way as before. The result: music that still has harmony, with the same pattern of shared partials as before, but without the integer ratios (or without the same integer ratios).
Music with non-integer ratios is not such an unusual thing after all. Piano strings, especially in small upright pianos, do not actually have harmonics at integer ratios to the fundamental. You can see that in the waveform if you look at it with an oscilloscope. The shape of the waves changes relatively slowly from the start of the note to the end, and not only by the loss of the high-frequency components - indicating significant partials at nearly, but not quite, integer ratios to the fundamental. Successive partials in a piano waveform tend to be a little higher than the corresponding integer multiples, to a degree that increases with increasing frequency. A computer scientist might say that instead of being proportional to n, the frequencies of the piano partials are proportional to n1+ϵ: slightly more than linear in their index. And to account for this effect, it's customary to tune pianos with stretched octaves. The notes at the top of the range are a little sharp compared to standard concert pitch, and those at the bottom a little flat, so that when you play two keys at once, the partials will line up and they will sound right together. It's easy to verify that pianos really do sound better when tuned this way; so why not carry the same principle further and see how far we can push it while still having the result sound like music?
Here's a simple tune. This is meant to be a round or canon at the unison, like "Row, Row, Row Your Boat." The idea is that after the first voice plays two measures, a second voice starts playing the same tune from the same pitch (at the point marked by the cross notehead), and then two measures later, a third voice starts, and so on, and we eventually end up with a two-bar phrase in four-part harmony that repeats for as long as we care to continue.
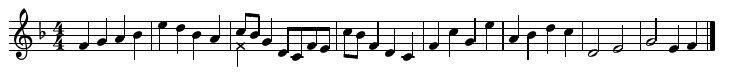
This tune is in the key of F and it uses ten different pitches, with their Helmholtz notation names, frequencies in Hz, and ratios to the root F as follows. Note that the music notation above is one octave higher than the actual frequencies, in order to make it fit nicely on the staff without a lot of ledger lines. You can pretend it's guitar music (with the standard one-octave transposition) if you want.
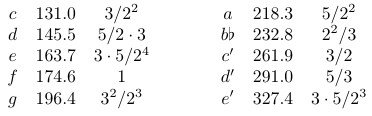
The frequencies in this table are exactly (up to the shown precision) in the ratios shown, and except for the root F, they are not the standard frequencies for these notes. Recall that near the start of this article I mentioned a D with a frequency of 293.7 Hz; but the table above places what should be that same note at 291.0 Hz instead. Why?
The answer is that, even apart from distortions like the stretched tuning of a piano, notes following the usual standard (which is called 12-tone equal temperament) are close to but not exactly in small-integer frequency ratios to each other. The standard frequencies for the notes are the result of a complicated centuries-old compromise in which several different important considerations are averaged out. First of all, the 2:1 frequency (called an "octave") ratio between two notes like c and c' is taken to be exact. These two notes (C, and C somewhat higher) are considered to be so much like each other that in some meaningful sense they are really the same note. Thy share the maximum possible number of harmonics (every harmonic of the higher one is shared with an even-numbered harmonic of the lower one). The 3:2 frequency ratio (called a "fifth") is also very important, so much so that it can be used as one way to define the frequencies of the different notes in the scale.
If you start at F and then go up a fifth, you hit C in the next octave. One fifth up from there is G, and then going up a fifth at a time from there, shifting down an octave whenever necessary, the next notes you hit are D, A, E, B, and then you're off the scale at a new note a little sharper than F - so it is called F#. Continuing further on this so-called circle of fifths, you hit sharp versions of the same letter names: from F# to C#, G#, D#, A#... and then E# is very close to F.
It would be really convenient to pretend that E# (defined as the note one fifth up from A#) was really at exactly the same frequency as F (defined as the note one fifth below C). Standard twelve-tone equal temperament is designed to achieve that by making all the "fifth" relationships a frequency ratio just a little smaller (flatter) than 3/2: namely 27/12, which is an irrational number approximating 1.4983. Many other ways of dealing with this issue exist. One nice thing about equal temperament is that it allows an instrument with fixed frequencies (like a piano or guitar) to play in any key equally well without retuning, and that in turn supports music that does clever things with swapping one interval in one key with a differently-defined interval in another key that happens to map onto the same notes - something that happens a lot in jazz.
Back to the frequency table: a principled way to change the frequencies of the notes and also the frequencies of the partials in order to maintain the harmony of the tune would be to redefine the values of the prime numbers. All the frequency ratios are stated in terms of powers of 2, 3, and 5. Similarly, we can factor the indices of the harmonics and define their frequencies in terms of primes, too: the fundamental is the fundamental, and then the next few harmonics are 2, 3, 22, 5, 2·3, and so on. (The next one uses a different prime, 7, but let's ignore that for now.) If we made "2" a little bigger in the table of note frequencies, and also used the same increased value of 2 in defining the partials of all the notes, then all the harmonics would continue to coincide in the same places even though the frequencies would be different.
More generally, the note frequency ratio table can look something like the following. Actually attempting to redefine numeric symbols like "2" would be a huge mess, not least because we also need to use those in exponents where they won't change, so I chose Greek letters more or less phonetically: τ tau for two, θ theta for three, and ϕ phi for five. With those changes the frequency ratios become as shown.
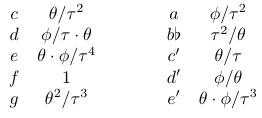
Frequencies for partials can be defined similarly: instead of 1, 2, 3, 4, 5, ... the partial frequencies can be 1, τ, θ, τ2, ϕ, ... With τ=2, θ=3, and ϕ=5, the partials are just standard harmonics and the notes of the melody are tuned to just intonation. With other values, both will change, quite possibly to the point that the partials end up out of order (like maybe partial number 5 at a lower frequency than partial number 4) and the contour of the melody changes a lot. The outline for a piece of music can consist of playing the tune, in round form with voices coming in and out, maybe varying the number of voices so it isn't so repetitive, and changing the values of the variables over the course of the piece to explore different inharmonic timbres while keeping the tune's tuning in line with the distorted spectrum.
Two other issues worth mentioning: for partials like number 7, where the index's factorization requires a prime other than 2, 3, or 5, I will just use the exact value without trying to vary it. And (in order to encompass standard 12-tone tuning within the range of things generated) I will not really use the same values of τ, θ, and ϕ for both melody and timbre. Instead, I will define three more variables τ', θ', and ϕ' for the melody and allow them to vary a little bit from the values of τ, θ, and ϕ used for defining the partials in the timbre. That simulates the way an instrument like an organ might have exactly-harmonic partials while being tuned to an equally tempered, or some other non-just, scale.
I used Csound to implement this idea. It's a programming language for building software synthesizers, a little like a modular synth with a command line interface. It is not my purpose here to give a detailed tutorial on Csound, but I'll highlight some interesting bits in the code.
I have one instrument that generates the values of the replacement-prime variables, like this:
instr 1 ktauc linseg 1200,24,1200,48,960,48,1440, \ 24,1200,19.2,1200,38.4,2786,19.2,2786,38.4,2786,19.2,2786,38.4, \ 1902,19.2,1902,38.4,1902,19.2,1902,38.4,1200,60,1200 kthetac linseg 1902,24,1902,48,1522,48,2282, \ 24,2786,19.2,2786,38.4,1200,19.2,1200,38.4,1902,19.2,1902,38.4, \ 2786,19.2,2786,38.4,1200,19.2,1200,38.4,1902,60,1902 kphic linseg 2786,24,2786,48,2229,48,3343, \ 24,1902,19.2,1902,38.4,1902,19.2,1902,38.4,1200,19.2,1200,38.4, \ 1200,19.2,1200,38.4,2786,19.2,2786,38.4,2786,60,2786 ktauo poscil3 15,1/11,gisintbl,rnd(1) kthetao poscil3 15,1/13,gisintbl,rnd(1) kphio poscil3 15,1/17,gisintbl,rnd(1) gktau=2^(ktauc/1200) gktheta=2^(kthetac/1200) gkphi=2^(kphic/1200) gktaup=2^((ktauc+ktauo)/1200) gkthetap=2^((kthetac+kthetao)/1200) gkphip=2^((kphic+kphio)/1200) endin
The six variables set at the bottom are global ("g") k-rate ("k") variables for tau, theta, phi, and primed ("p") versions of them. The unprimed versions are all set by linear envelope generators (the "linseg" opcode) to set a general outline of the piece as follows: at the start, it uses pure harmonics briefly to present the melody by itself. Then it starts in with the round, and all the variables decrease, so that the partials will collapse to lower frequencies (compressed octave) and so will the melody steps. Then it increases all the partials until the octaves are stretched far more than any piano. After that, it starts shifting around the values of the variables, to briefly stop at all six different permutations of 2, 3, and 5 for the three variables, with periods in between where they move to the next permutation. Internally to the instrument, the values are measured in cents (logarithms to the base 21/1200 or about 1.00058); so the last step in the calculation is an exponentiation to convert those into raw ratios.
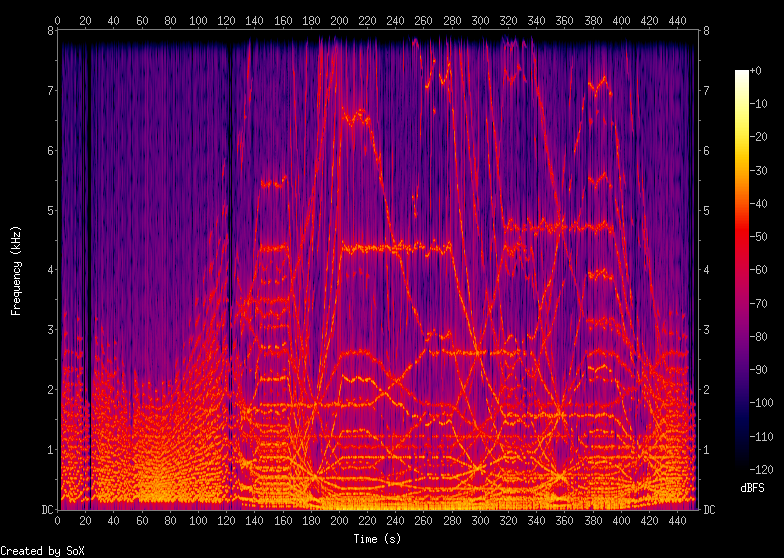
Jumping ahead of myself, but the motion of the partials is quite visible in this spectrogram of the finished piece. First the spectrum gets squashed, then stretched, and then different pieces of it are pulled out and rearranged.
Instrument 2's code is long, and I won't paste it in right here, but the first thing it does is decide whether to run at all. It is assumed invoked at the point where one of the voices could come in (i.e. at the start of an odd-numbered measure). It takes a parameter which is the probability of starting another iteration of the melody, and it triggers with that probability except that it will not allow the piece to go silent: if no other iterations are running, then it necessarily starts a new one. And when it decides to start a new iteration, it uses the Csound "schedule" opcode to push 33 invocations of instrument 3 into the buffer of upcoming notes, for the 33 notes of the basic melody.
Instrument 3 is never invoked directly by the score, only by the scheduling in instrument 2. But when it runs, it starts by determining its fundamental frequency, with a simple if/elseif cascade that covers just the ten pitches needed. There is a little bit of randomization applied in order to avoid unwanted cancellation effects if two notes at the same pitch end up being played at once.
instr 3 ifm=184.997211+birnd(1.5) if p4 == -3 then kfreq1=ifm*gkthetap/(gktaup*gktaup) elseif p4 == -2 then kfreq1=ifm*gkphip/(gktaup*gkthetap) elseif p4 == -1 then kfreq1=ifm*gkthetap*gkphip/(gktaup^4) elseif p4 == 0 then kfreq1=ifm elseif p4 == 1 then ; etc...
Then it computes frequencies for all the partials up to index 10. Note the use of plain 7 as the ratio multiplier for the seventh harmonic. Because we don't go as far as partial 11, 7 is the only partial not open to distortion.
kfreq2=kfreq1*gktau kfreq3=kfreq1*gktheta kfreq4=kfreq2*gktau kfreq5=kfreq1*gkphi kfreq6=kfreq2*gktheta kfreq7=kfreq1*7 kfreq8=kfreq4*gktau kfreq9=kfreq3*gktheta kfreq10=kfreq2*gkphi
The rest of instrument 3 is just a straightforward additive synthesizer with ten fixed envelope generators and ten oscillators. Finally, instrument 1000 (given a higher number to make sure it runs last in Csound's internal loop) takes the output gathered from the instances of instrument 3, runs it through all-pass filters to eliminate spikes, a soft clipping function (which has very little effect in this particular piece) also to deal with excessive spikes, and finally a little bit of reverb.
instr 1000 aphl phaser1 galeft,330,6,0 aphr phaser1 garight,330,6,0 galeft=0 garight=0 aleft table3 aphl*0.03,gicliptbl,1,0.5,0 aright table3 aphr*0.03,gicliptbl,1,0.5,0 arevl,arevr reverbsc aleft,aright,0.67,9000,sr,1.0 outs aleft+0.2*arevl,aright+0.2*arevr endin alwayson 1000
Here is the finished piece as a stream, and its Csound code.
◀ PREV Modular synthesis intro, part 11: Digital oscillators || Modular Synthesis Intro, part 12: Sequencing NEXT ▶
