DACs and bit count
2023-11-14 electronics digital MSK 014
The connections between modules in a modular synthesizer are made with analog voltages, both for audio and control signals. Many popular modules use digital processing internally, but they need to convert to and from analog voltages to communicate with other modules. Even a non-modular synth that might use entirely digital signalling internally, has to convert those signals to analog at some point in order to drive a speaker. So digital to analog converters (DACs), and the corresponding analog to digital converters (ADCs), are important in synthesizers and people say and think many things about them, not all of which are correct.
This article is the first in a three-part series on DACs and how many bits they have. That's not the only interesting thing to talk about with regard to conversion between analog and digital. ADCs have their own considerations, and sampling rate is relevant to both. I may go into those things in future articles.
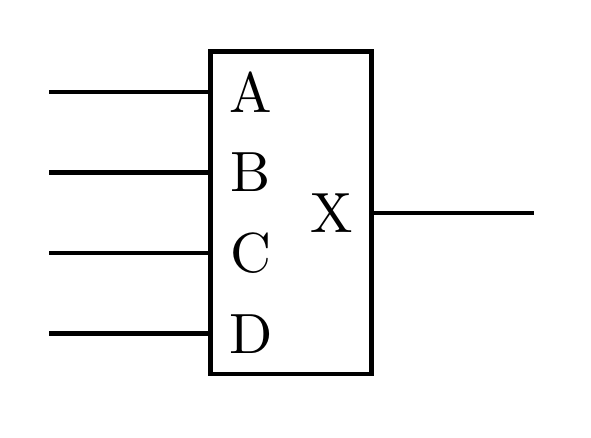
The usual image of a DAC is that of a black box with several bits of digital input and one analog output. When it's drawn that way, it looks like a straightforward thing that ought to be available as a building-block IC, easy to build into a circuit, with very little that could go wrong with it.
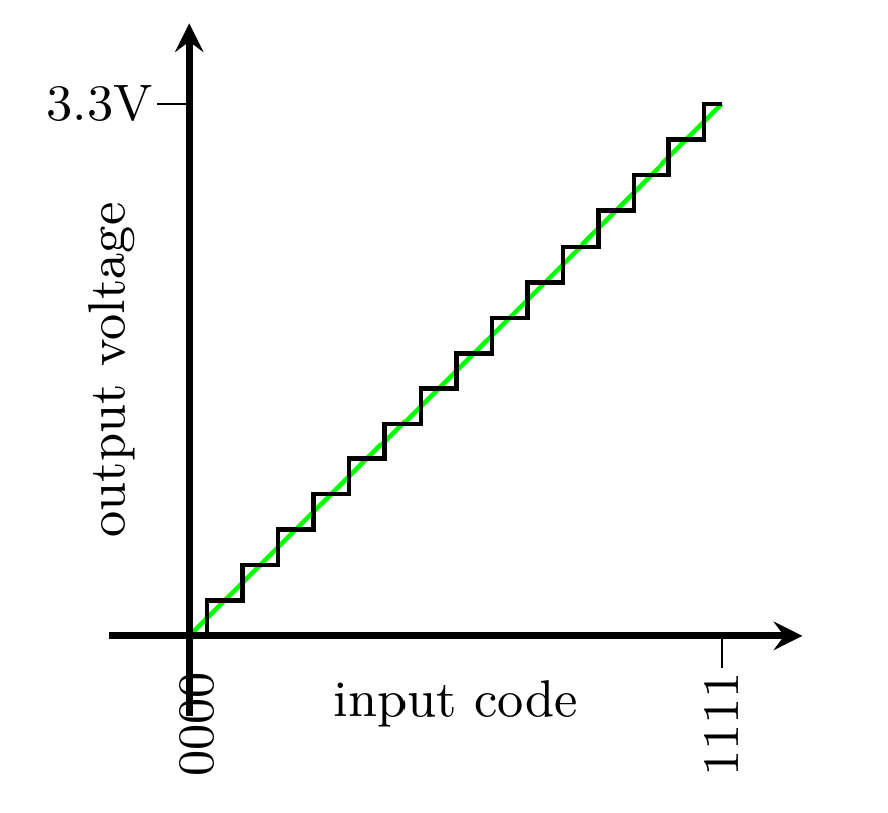
A digital signal is typically 0V to mean logic 0 and some specific positive voltage, like maybe 3.3V, for logic 1. Then the output of the DAC is supposed to be a voltage in a specific range, proportional to the binary value of the digital input. For instance, maybe you have a 4-bit DAC with an output range of 0.0V to 3.3V, and then on input code 0000 it gives 0.0V output, on 1111 it gives 3.3V output, and on a code in between, like say 0101, it gives an output voltage proportionally between those two (calculation: (5/15)*3.3V = 1.1V output for code 0101).
If you think through the math carefully, you can come to the realization that the output voltage of this example DAC is just a weighted average, or sum of scaled versions, of its input voltages. If the four input voltages are A, B, C, and D, then the output voltage is 0.533A+0.267B+0.133C+0.067D. Those coefficients add up to 1.000. So it might seem that you don't even need active electronics to build it. The DAC could be just a resistor network! Just using a resistor network doesn't really work well in practice, because the voltage levels of digital signals are usually not very accurate (the inputs might not really be exactly 0.0V for 0 and 3.3V for 1), and you'd probably also want some kind of buffer on the output so changing loads don't throw it off. But it still feels like building a DAC should be easy, almost trivial. If it's not just a resistor network, then it's not much more. And indeed, real DACs often are based on resistor networks; but they are not quite so simple.
How many bits?
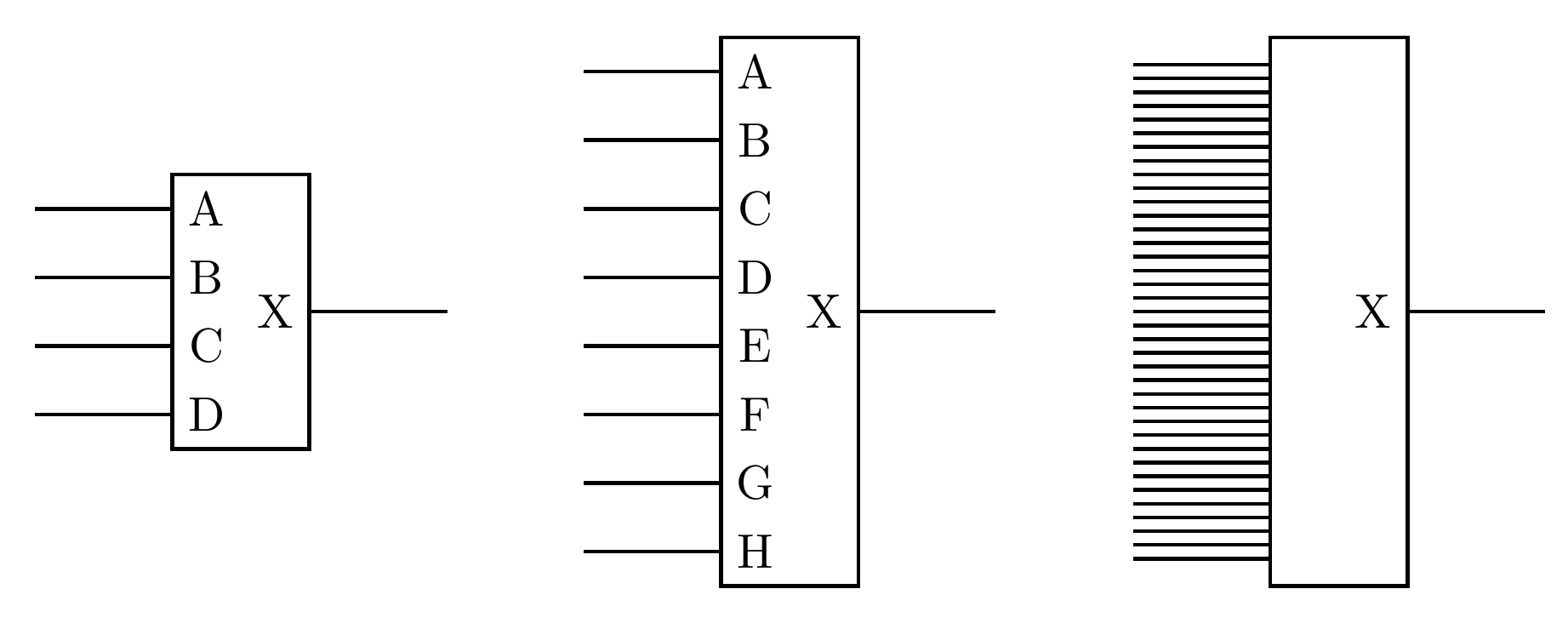
What differences exist between DACs that could lead you to choose one over another? At the black box level it seems like there aren't many. There could be differences in the voltage levels they expect at the input (like 3.3V or 5.0V logic). There could be differences in the voltage ranges they produce at the output. Someone might have a vague idea that some DACs can handle faster or slower signals, but there's nothing in the black-box circuit diagram to suggest timing is relevant to a DAC at all, and at first glance it might seem there should be no practical limit on a DAC's speed. But there's one thing that obviously makes a big difference: the number of lines you draw going into the box. That is the number of bits in the digital input, and it's an important specification for a DAC.
If you have n bits of input, then you have 2n different codes. With 4 bits, there are 16 codes. With 5 bits, there are 32 codes. It doubles for each additional bit. The number of codes is also the number of different voltages the DAC can produce, and therefore (with the assumption the voltages are equally spaced) the number of codes is inverse to how accurately you can get the DAC to produce a desired voltage on its output.
In my earlier example of the 4-bit DAC with 16 different codes, the spacing between possible output voltages was the 3.3V range divided by 15 (one less than 16 because of using a code for zero) and therefore 0.22V; it could hit a desired voltage within the output range to within ±0.11V. For each additional bit, the error would be cut in half. With 8 bits, it could achieve ±6.5mV accuracy - assuming there were no sources of error other than the number of bits itself. With 16 bits, it seems like it could be ±25µV.
If we're using a DAC to produce a DC control voltage, then this calculation from the number of bits tells how accurate the voltage can be, as a best-case theoretical limit that isn't dependent on any details of what kind of DAC it is, how good the implementation is, the quality of support circuitry, or similar. If we're using the DAC to produce a changing signal, like to play back an audio sample, then the voltage inaccuracy can be thought of as noise: it appears as an effectively random wideband signal added onto our desired signal. Then the same calculation can be used to describe the best possible signal-to-noise ratio (SNR) for the output. It can also be thought of as a calculation of dynamic range: the ratio between a single code step in the DAC input and the full range, is the amplitude ratio between the softest signal the DAC can generate other than silence, and the loudest.
Here are some numbers, assuming a theoretically perfect black-box DAC with 3.3V output range.
| bits | codes | V | SNR |
|---|---|---|---|
| 4 | 16 | ±0.11V | 23.5dB |
| 8 | 256 | ±6.5mV | 48.1dB |
| 12 | 4096 | ±400µV | 72.2dB |
| 16 | 65536 | ±25µV | 96.3dB |
| 20 | 1048576 | ±1.6µV | 120.4dB |
| 24 | 16777216 | ±98nV | 144.5dB |
| 28 | 268435456 | ±6.1nV | 168.6dB |
| 32 | 4294967296 | ±0.38nV | 192.7dB |
The designers of the Compact Disc format settled on using 16-bit samples, which were at the limit of what the technology could handle at the time, largely for reasons of dynamic range. That's about the limit in audio quality of what the most sensitive human ears can hear. Human ears have not gotten better in the decades since then, but a lot of more recent digital systems use 24-bit sample formats, partly because they can, partly to provide extra headroom for processing without quality loss internally to digital workflows, and partly, perhaps unfortunately, for marketing reasons. It sounds sexier, especially to someone who half-knows that each bit means another 6dB of some sort of "quality," to say that a product has 24 bits in comparison to old-fashioned CDs that have only 16. And then why not 32 bits? Why not even more?
I've had people write to me asking if I had "24-bit" versions of the (lossily compressed, streaming MP3) module audio demos from my storefront, clearly convinced that they'd be able to hear important things in such files that they couldn't hear in the files as they are currently posted. I was tempted to say "yes" and send copies of the same files reencoded to a 24-bit sample width and maybe with some extra noise added, but I just said "no, sorry." I've also seen someone on a Web forum pick a fight with the founder of Mutable Instruments over whether what they alleged was the "14-bit" sample resolution of the Clouds module (actually a 24-bit CODEC running in 16-bit mode) caused its audio quality to be "shit."
There's a similar pressure for greater bit width in DACs used to generate control voltages. If you are generating pitch control voltages over let's say a 5V range, then a 12-bit DAC's theoretical accuracy is ±610µV (not the same as the number in the table above because referenced to a different range). That's equivalent to about ±0.7 cents of pitch on a V/octave pitch CV, and well beyond the capabilities of human pitch perception (typically 5 cents resolution at best); it should be plenty for pitch CV. But it is routine for synthesizer users to turn up their noses at 12-bit DACs in CV-generating modules as "not accurate enough."
And why not? If audio is routinely 24-bit, then why shouldn't we also have 24-bit DACs for control voltages? Why, in fact, don't we? Why does the North Coast Synthesis Ltd. MSK 014 Gracious Host, a carefully-designed module, use only 12-bit DACs - what would be lost by specifying a wider chip? Conversely, if there are important reasons not to use more than 12 bits for control voltages, then why do people bother using 24 or even 16 bits for audio? Don't the same issues also apply to audio DACs?
Why not just draw more lines into the box on the circuit diagram?
The realities of 24-bit voltage accuracy
One important part of the DAC bit count puzzle is that audio isn't a DC voltage, and low-noise audio is not the same as ultra-accurate DC voltage. Let's think a bit more about what it would mean to have extremely precise control voltage generation, and the other things we would have to think about in order to make good use of such a capability.
In an important practical sense, 24-bit voltages don't even exist. When we're talking about measuring or generating voltages with a precision of four or five decimal digits (13 to 17 bits), it makes sense to say "the voltage on this wire is such and such" as if that were true for the entire wire and would remain true, if not for all time, at least for a little while. But the statement doesn't extend so far in time or space when we try to make it at higher precision. We can only talk about the voltage at a specific point on the wire, and at one particular moment, if we're talking about voltage at 24-bit precision.
A typical Eurorack patch cable might be made with 22-gauge copper wire, which has a resistance of about 16mΩ per foot (0.5mΩ per cm). Comparing that to the 100kΩ typical impedance of a Eurorack module input, it means that changing the length of the patch cable by one foot will make a difference of 0.16ppm (parts per million) to the voltage seen at the module input. The base-2 logarithm of that is about -22.6, meaning the difference caused an additional foot of cable length is slightly smaller than one code count in the output of a theoretically perfect 22-bit DAC.
If you can't hear the difference between using a one-foot or a two-foot patch cable when all other things are equal, then you can't hear 23 bits of voltage resolution, and conversely if you had a DAC with more than 22 bits of voltage resolution, then you'd need to control all your cable lengths to better than a foot in order to preserve the DAC's accuracy. Allowable error is cut in half for each additional bit, and is sub-millimeter for 32 bits.
The highest-resolution digital benchtop multimeter with a definite price tag that I could find in a quick skim of a couple of vendors' Web sites was the Keithley 2002, which has a base price of $14,100.00 Canadian. (Calibration service is a separate charge.) It advertises "true" 8.5 decimal digit accuracy, which is equivalent to about 28 bits. It is also described as containing a 28-bit ADC. But if you read the data sheet, there is a lot of relevant small print.
To get the best possible DC voltage accuracy from this or any similar high-accuracy voltmeter, you need to use "transfer" measurement procedures. You first measure the apparent voltage of an accurate reference voltage close to the one you're measuring, then you measure the apparent voltage of the thing you actually want to measure, then you calculate the ratio between them. Of course, you have to have an accurate voltage standard available to measure against in the first place. You also have to use the right probes and cables, and the same probes and cables, for both, and make both measurements within 10 minutes of each other, and keep the meter and the probes within 0.5°C of the calibration temperature throughout. And deal with thermocouple effects where your metal probes touch the metal things you're measuring. And give the meter four hours to warm up before doing this, and of course don't power-cycle anything during the procedure. If you follow all the rules, then in the operating mode and voltage range which give the most accurate results, the $14k multimeter is specified to have an accuracy of 0.1ppm of the measurement, plus 0.05ppm of its 20V full scale range, plus of course whatever is the uncertainty in your reference voltage source. Best case, a total of 0.15ppm, which is equivalent to about 22.7 bits. Assuming you follow all the rules, and you have a perfect voltage reference to measure against.
I couldn't find a useful specification for the Keithley 2002's absolute accuracy - that is, if you just plug in a voltage and ask the multimeter to measure it without doing the transfer procedure. It probably depends on which calibration service you bought and how recently, but it certainly won't be any better than the "transfer" specification, which represents the most accurate possible way to use the meter. Absolute measurement against the meter's internal reference is not the preferred method. Also note that the 2002's specified relative accuracy for ratio-based measurements declines to 1.2+0.1ppm (19.6 bits) over a 24-hour period, and 6+0.15ppm (17.3 bits) over a 90-day period, again both of those under optimal conditions.
When we're talking about voltage measurements beyond about 20 bits, very small physical effects come into play. I mentioned the resistance of patch cables. Pretty much all electronic components change their parameters in response to temperature, and that includes both the components in the DAC and in whatever you plug it into (a measuring device, or a module to be controlled with CV). That's the reason for the rules about keeping the fancy multimeter near its calibration temperature: the calibration won't be valid if you don't. Components also change over time - not very fast, but fast enough that their changed values show up on a scale of days or hours once you're demanding extremely high precision. Random differences in the physical setup from one measurement to the next, like exactly which spot on the patch cable plug was hit by the contact when you inserted it into the socket this time, are also going to create random voltage effects large enough to swamp a theoretical accuracy of 24 bits.
So if you had a 24-bit DAC with 24 real bits of DC voltage accuracy, never mind 32 bits, how would you even know? You can't hear 24 bits; a $14k special high-precision multimeter isn't good enough to measure 24 bits; the connections between this DAC and other equipment would introduce enough error to spoil the precision; supposedly-unchanging DC voltages are moving targets at the 24-bit level; and so you'd have no way of telling the difference between the DAC that was really 24 bits and another one that was less accurate.
The ultimate in voltage precision, the most accurate voltage available with present-day technology at any price, would be a metrological "primary standard" voltage reference, based on superconducting Josephson junctions driven by a microwave source at about 75GHz. That's the kind of thing used in national standards labs. You can buy your own primary voltage standard from HYPRES, with your choice of a liquid helium cooling system or closed-loop cryocooler. The accuracy they advertise, for the most accurate configuration, is 0.005ppm. That's equivalent to about 27.6 bits.
The dollar price for the primary voltage standard is not listed on the HYPRES Web site. NIST, a US government agency, seems to be offering a similar instrument which may be even a little more accurate, for about US$320k depending on configuration; I don't know if that price (on a Web page dating from 2016) is still current or available to the general public internationally.
As for size, from the photos it appears that the smallest complete HYPRES configuration fills a standard half-height (21U) server rack. That's the same kind of rack which could hold seven 84HP rows of Eurorack modules. So we can say it's 588HP, not counting the liquid helium dewar, the dedicated desktop PC for controlling it, or the high-precision multimeters (starting at $14k a pop) you might be calibrating with it. And that's for just over 27 bits.
But some people still think they really want 24 or even 32 bits from a portable music-synthesizer DAC, and they think they can get that. They expect 24 bits from a Eurorack module on a Eurorack power supply, without liquid helium cooling, for less than $200 and 6HP. And there are manufacturers who claim to provide this. At the component level, Mouser's parametric search turns up hundreds of CODEC chips incorporating multiple channels of both analog-to-digital and digital-to-analog with claimed 24- or 32-bit resolution, including dozens of types priced at less than $5 each. Many popular digital Eurorack modules do contain such chips. How are such things possible?
The less polite answer is that the manufacturers are lying outright. The more polite answer is that they are truthfully reporting a different specification that happens to also be expressed in bits but is not the same thing as absolute DC voltage accuracy. One of the clues is in the fact that I switched from saying "DAC" to saying "CODEC" there. In order to get the full story, we'll have to break open the black box and go into how these devices actually work. That is the subject opened in the second part in this series: DACs, resistors, and switches.
◀ PREV Inrush current and measuring it || DACs, resistors, and switches NEXT ▶