All about levels

2022-12-04 electronics design

There's a lot of confusion in the modular synth world about signal levels. We often don't have a clear idea of what can plug into what, even within the modular rack; let alone when it comes to interfacing with other equipment. I've been working on guitar pedal designs recently and connections between those and modular often raise level-conversion issues. A whole lot of unnecessary "external input" and "external output" modules are sold to newbie wigglers who've been told that modular and other-equipment levels are fundamentally different and need to be converted - but although usually unnecessary in most modular racks, such modules do also serve useful purposes in certain contexts. What is really going on with signal levels? In this article I'll go through some of the concepts used for describing signal levels accurately, then talk about some of the levels commonly seen in audio work.

Give "voltage range" a rest, please

I think part of the problem with levels in Eurorack is that synth users are inclined to think in terms of "voltage range" and they confuse that with signal level. I've said before and I'll keep saying it: "voltage range" is the wrong way to think about signals, especially in the context of using analog electronics.

When you are designing a circuit as opposed to using it, okay: sometimes you do need to think about the minimum and maximum voltages it can handle. When you are dealing with DC control voltages, sometimes it's useful to think about the range they might cover, but even that is less useful than people think. In day-to-day use of audio equipment, you'll usually only confuse yourself by trying to describe audio signals in terms of their minimum and maximum voltages. Signals are better described in terms of levels, which relate to voltages in a more complicated way that I'll describe below. In normal use, signals should not be going anywhere near the clipping limits of the gear, and the differences between strong and weak signals are not best described by reference to those clipping limits.

It's for this reason that proposals to standardize "voltage range" for modular inputs and outputs; complaints over the supposed catastrophic problem that such standardization has not already occurred; demands to print "voltage range" on front panels; databases of voltage ranges; and so on, are all misguided.

A related issue, but not one I'll cover in much detail here, has to do with the impedance at which voltage is measured. Eurorack users in particular usually talk about signals in terms of the open-circuit voltage of the output, assuming either a zero output impedance, an infinite input impedance, or quite often both. Open-circuit voltage is usually a reasonable approximation of reality in the Eurorack world, where output impedances are typically much lower than input impedances; but it would only be exactly correct to use open-circuit voltage if the impedance ratio between output and input were infinite, which is never really true. The true magnitude of the voltage on the connection between an input and output is always a little less than the hypothetical open-circuit voltage; and most of the time, that's just fine.

When some Eurorack users decide they aren't willing to settle for a reasonable approximation and want to describe voltages exactly, they tend to treat the fact of finite impedance as some kind of exception. Much of the talk around buffered multiples, "voltage droop," in-the-loop or out-of-the-loop protection resistors, and so on, has to do with this gap between the ideal of open-circuit voltage and the reality of connecting inputs to outputs. In other fields of electronics, people are more likely to accept that real inputs have finite impedance, and measure voltage with respect to a standardized input impedance rather than assuming open circuit voltage as the normal default from which anything else is a compromise.

You can read a bit more about impedance and its relationship to voltage in my earlier article on equivalent circuits.

Voltage is more than a "range"

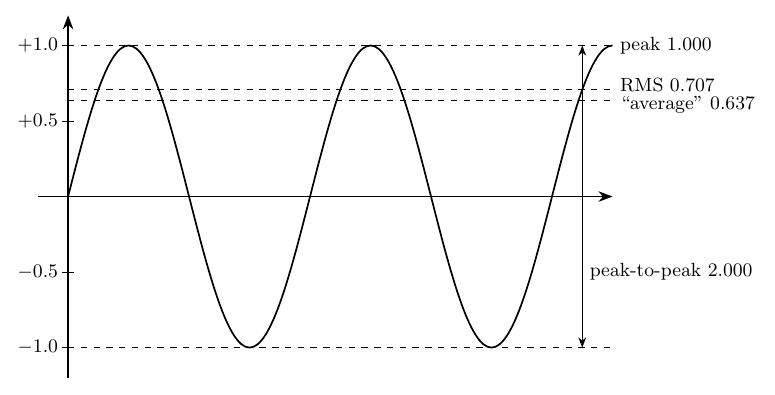
Here's a sine wave with a "range" of ±1V. I've marked a couple of other voltages of interest on the diagram, too.

The easiest thing to measure when viewing this waveform on an oscilloscope is the height of the peaks, and it's quite natural to think of this sine wave's amplitude in terms of the height of those peaks. It doesn't matter much whether we look at maximum distance from the centreline (1.0V) or the peak-to-peak distance (2.0V), as long as we remember which measurement we are using, because the waveform is symmetric. And knowing the height of the peaks makes it easy to know how close we are to clipping, by comparing against the "voltage range" of whatever equipment we're feeding the signal through.

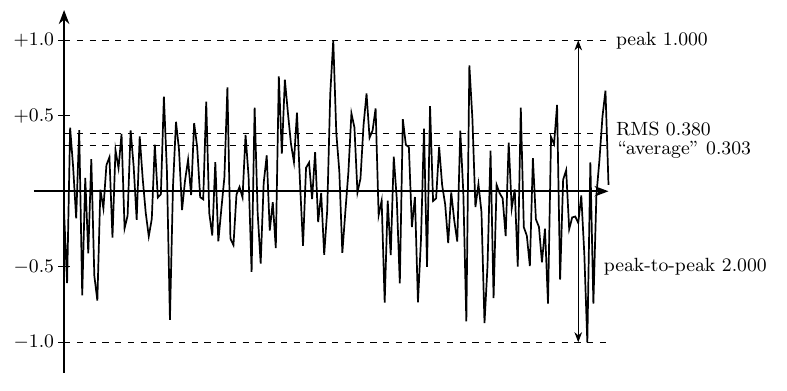
But now look at a more complicated waveform. A Eurorack oscillator might produce a pure sine wave with just one frequency in it, but after we start doing modulation, filtering, shaping, and mixing, the real audio signal in a modular patch will likely contain a mixture of different frequencies. When the peaks of two or more frequencies in the same direction happen to collide, they will add up to a higher voltage; when peaks in opposite directions collide, they will cancel. So the mixed signal tends to be a complicated thing with peaks of many different heights. It will stay near the centreline much of the time, with occasional spikes further out. I have simulated that by sampling random voltages from a normal distribution to make this illustration. Real musical recordings (what people call "program material") look a lot like this over short time scales. Over longer periods there is even more variation in program material because of note envelopes, silences between notes, louder and quieter bits, and so on.

The peak-to-peak range of the program material is the same as for the sine wave; but is that really a good way to describe the level of the waveform? The voltages here mostly stick around zero, much more so than the sine wave does. I've measured the peak voltage, over the time interval shown, but instead of repeatedly hitting the same peak at regular intervals, this waveform hits its peaks rarely, at random. It should be clear that those peaks are just the highest and lowest voltages that happened to occur in the time covered by my sample. If you took another sample later, it might hit a slightly higher peak. Or it might not hit a peak as high as this one. The longer we spend measuring the signal the wider its peak-to-peak range will appear, as we get the chance to witness rarer and rarer unusually high peaks. With the normal distribution I was sampling from, the long-term maximum and minimum are technically infinite, though it would be extremely rare to see any peaks far outside the sample in the picture.

Also, clipping is not the beginning and end of why we might care about the loudness or level of a signal. If you were putting the above random signal through a module or a mixing board with an (unrealistically small) clipping range of ±1V, you might reasonably decide to turn up the gain a bit and let it clip at the rare peaks, in order to get more volume during the large majority of the time when it's confined within a much smaller range. You probably wouldn't hear that small amount of clipping. Doing such a thing with the sine wave, on the other hand, would cause clipping on every single cycle and a lot of audible distortion.

And once clipping is in effect, the minimum and maximum voltage are fixed but the level can still meaningfully change. There's an important distinction to be drawn between the relatively low level where the signal is just barely and rarely clipping, usually still near zero, and the higher level where it's clipping all the time and usually far from zero. Peak-to-peak measurement says those two signals are at the same level, but in an important way which we should be able to measure, they are not. We need a different way to describe signal level beyond just the range between minimum and maximum voltage.

Searching for the usual voltage

We need a different way to describe level, and I've already hinted at it: signal levels are best described not by their peak voltages but by their usual voltages. Is the voltage usually near the centreline (conventionally zero)? Or is it usually further away? Answering the "usual voltage" question tells us the level of the signal in a more useful way than looking at the range from peak to peak.

The obvious way to find the "usual" voltage is to define it as the average voltage, but actually doing that creates some technical problems. First, audio signals are usually centred on zero, going positive and negative pretty much equally in both time and voltage. Centering on zero is especially true after the signal has passed through an AC coupling capacitor. The average voltage of such a signal will just be zero! And even if you add a DC bias to the signal to centre it elsewhere, which is often done in electronic design for various reasons, the time-average of the voltage will end up being equal to that DC bias, telling you nothing useful about the signal itself.

The obvious way to solve that problem is to take the average of the absolute value of the signal, or the distance from the centreline. If the voltage at one moment is +1V, we count that as 1, and if the voltage is -1V we also count that as 1. Subtracting out any DC bias before this calculation would be a good idea, if the signal was not actually centred on zero to begin with.

I have marked the level calculated that way on my diagrams: the "average" voltage for the sine wave is 0.637V and for the normal-random signal it is 0.303V. I put "average" in quotes because, again, this is actually the time average of the absolute value, with negative voltages treated as positive; the plain average would just be zero. From these numbers we can correctly recognize the fact that the sine wave is the stronger of the two signals despite having the same peak-to-peak range as the random signal.

The "average" defined this way will be stable over long samples from the spiky random signal; rare high peaks, because they are rare, will not spoil it the way they would spoil the maximum-voltage measurement. And the "average" voltage will correctly describe the way a signal can continue to get even stronger beyond the point where its peaks are being cut off by clipping.

A better average

The average of the absolute voltage is not really the best way to describe level, nor is it the standard way used in most engineering situations, because some important technical issues remain. The absolute value function is not differentiable at zero; without going into any depth on what that means, this fact makes it annoyingly hard to do calculus on signal levels expressed in terms of the absolute value of the voltage. Mathematicians would prefer to use a definition in terms of smooth curves if possible.

A physical effect may be even more important: the power level of a waveform, measuring things like how much physical energy is consumed in doing things with the voltage, actually scales with the square of the voltage, that is, voltage times itself. If you apply a voltage to a fixed resistance, then because the power is voltage times current, and the current is proportional to voltage, therefore the power going into the load ends up being proportional to the square of the voltage. Double the voltage and you get four times as much power, not only two times.

So if we want to measure the level of a signal in a way that has physical reality to it, and keep the mathematicians happy, then it seems we should really be giving more weight to the peaks than to the voltages near zero, even though I've just argued at length why we shouldn't give all the weight to the peaks. We want to do some kind of weighted average, weighting peaks more but all voltages somewhat; and we want to do it using a function that is everywhere differentiable so the calculus won't become too complicated. Using the square of the voltage works well.

The standard way to measure signal levels, and the best way in most cases, is with something called RMS voltage. RMS stands for "Root-Mean-Square," which summarizes how it's calculated. RMS voltage is:

• The square ROOT
• of the average, which is technically called the MEAN,
• of the SQUARE of the voltage.

I've marked the RMS voltage on the diagrams too. For the sine wave, it is 0.707V (which you might recognize as half the square root of two); for the normal distribution sample it is 0.380V. RMS voltage may not seem very intuitive at first, but it has a natural physical basis: the RMS voltage of an AC signal is the equivalent DC voltage that would dissipate the same power in a fixed-resistance load.

In most electrical engineering contexts, RMS voltage is understood to refer to the voltage across the load under real-life impedance conditions - not the open-circuit voltage of the source, although when the source has a much lower impedance than the load, those two voltages will be approximately the same.

The ratio between the RMS voltage and the (one-sided) peak voltage is called the crest factor and it's important when we want to convert between RMS and peak-to-peak descriptions of signal level. As shown by the examples above, crest factor depends on the waveform; so there is no fixed conversion factor between RMS voltage and "voltage range."

The crest factor for a sine wave is 1.414 (square root of 2), as described above. For a sawtooth it's 1.732 (square root of 3) and for a square wave it's 1.000. Crest factor for real program material will vary a lot, but the normal distribution is halfway reasonable to use as a default assumption for estimating voltages of program material because (by the Central Limit Theorem) mixing many spiky signals with potentially different crest factors together will tend to approach a normal distribution closely as one adds more and more signals. Normally-distributed random voltages theoretically have an infinite crest factor because there is no limit to how high a peak in such a signal might be; but if normal distribution seems like a reasonable assumption, then we might also choose to use a 99% interval - that is, choose bounds such that the signal will be within the bounds and not clipping, 99% of the time. That would imply a bound on each side, functioning like the crest factor, at 2.8 times the RMS voltage.

Decibels

There's one more important concept to introduce before we can talk intelligently about signal levels, and that is their logarithmic description using decibels. I think most readers probably already have some understanding of how decibels are used, so this section is more a reminder than a detailed introduction.

Decibels are a unit of measurement for proportion, with the abbreviation "dB." Adding ten decibels (+10dB) means multiplying some relevant quantity by ten; subtracting ten decibels (-10dB) means dividing the quantity by ten. Note that adding 20dB does not mean multiplying by 20; it means multiplying by 100, because it's the same as adding 10dB twice. The numbers work out in such a way that adding or subtracting 3dB also corresponds almost exactly to multiplying or dividing by 2.

Why use decibels? In audio we often have to deal with wide dynamic range in different parameters. The difference in power between the softest sound detectable by a human ear, and the sound level that causes immediate injury, is a factor of 1,000,000,000,000; calling that factor "120dB" is more manageable than trying to switch between different metric prefixes on the units while working at different scales, or dealing with a lot of zeroes on either side of the decimal point.

Moreover, something we often want to do with signal levels is keep track of the gains and losses from chaining together things like amplifiers, filters, and so on. Expressing the levels in decibels makes that easy because it changes multiplication into addition. Maybe there is an amplifier that multiplies the power of a signal by 1.58. Rather than having to take the number of milliwatts at the input and do a multiplication to get the milliwatts at the output, it's easier to know that that amplifier adds 4dB to the signal level. If evaluating a system with many stages that impose gains and losses on the signal level, the convenience of adding and subtracting decibels instead of multiplying and dividing RMS voltages is significant.

One gotcha with using decibels to express signal levels is that people normally want to talk about the power of a signal (voltage times current) even though they measure signals by RMS voltage. Power, at a fixed impedance, is proportional to the square of voltage. So if you take the voltage and multiply by 10, you haven't actually added 10dB; you have added 20dB. Similarly, doubling or halving the voltage means adding or subtracting 6dB, because you are applying a factor of four, not two, to the power. Adding 10dB would only increase the RMS voltage by a factor of 3.16 (the square root of 10). I said 10dB corresponds to multiplying by ten, but it refers to power, not voltage.

Another gotcha is that, as you may have noticed, I've been referring to adding and subtracting decibels, but not to where the levels orginally come from. A number of decibels as such only describes the difference between two signal levels. How will we describe the level of just one signal?

To describe the level of one signal, we need a reference point. Some signal level has to be defined as zero decibels, and then any other signal can be described as so many decibels above or below the reference.

One popular scale is called "dBV": decibels referenced to volts. A 0dBV signal has an RMS voltage of 1V. On that scale, the sine wave illustrated earlier (2.000V peak to peak, 0.707V RMS) has a level of -3dBV: it is half the power of 1V RMS. There are simple formulas for converting between RMS voltage and dBV.

• dBV = 20 log₁₀ V_RMS
• V_RMS = 10^dBV/20

But an even more popular scale, originating with the Bell telephone company, is called "dBu" and defined by 0dBu = 0.775V RMS. That somewhat peculiar-sounding reference level was chosen because 0.775V is the RMS voltage that will deliver 1mW of power into a 600Ω load, which was a very common impedance level for telephone and (at the time) audio equipment. The dBu scale is the one you'll most often see used to describe audio signal levels, especially in the context of synthesizers.

Using the above formulas you can easily determine that 0dBu = -2.21dBV, and that is the conversion factor between the two. To convert a level in dBu to dBV, subtract 2.21; to convert from dBV to dBu, add 2.21.

Pay close attention to the capitalization: it is "dBV" with a capital V and "dBu" with a small u. Apparently, when dBu was first introduced it was actually intended to be "dBU" with a capital U, but the confusion between dBU and dBV proved to be too great and so they changed it to "dBu." There is no commonly-used "dBv" scale with a small v, and you should avoid writing that (or "dBU" with a capital U nowadays) because it is ambiguous whether such an abbreviation might be interpreted as dBu or dBV.

It is also, always, a small "d" and a large "B." The rationale here is that a "decibel" is actualy defined to be one tenth of a "bel," where a "bel" is a unit rarely used by itself that corresponds to multiplying by ten, and "deci" is a metric-style prefix meaning "one tenth of that." The "deci" prefix is always abbreviated with a small "d," and although the "bel" is not an SI unit, it is given a capital letter according to the SI convention because named after a person (Alexander Graham Bell).

Signal levels

The lowest signal level you're commonly going to find in audio is so-called "mic level": the signal that comes from a microphone. Mic level varies a lot depending on the microphone, but is usually about -60dBu to -40dBu. Or dBV; it's vaguely defined enough that the 2.2dB difference in these two scales is insignificant. Those numbers would correspond to anywhere from 775µV to 10mV RMS. Because mic level is so low, microphones often require preamplifiers to bring the signal up to a level other equipment can use; and the unamplified cable from the microphone to the preamplifier tends to be especially sensitive to interference and needs to be kept short and well-shielded. Some types of microphones operate at very high impedance, but in that case they usually need built-in preamplifiers and don't have a cable operating at the original mic level at all; when there is a cable carrying signal at mic level, the impedance is usually relatively low, under 2kΩ or so.

The cable between a guitar, bass, or similar and its amplifier carries a signal at "instrument level." This is the level the guitar produces and the amp expects. Effects pedals are designed to use instrument level for both input and output. This is still a low level, and still somewhat variable, but it's higher than mic level and a little more consistent. I've seen different ranges quoted by different sources but a typical value might be -20dBu to -14dBu, corresponding to about 80mV to 160mV RMS - depending on the pickups and how hard you play. Effects often give output voltages a little higher, and there may be spikes considerably above the RMS voltage, so it's usually expected that equipment operating at this level ought to have a fair bit of headroom. (Another reason is that some people want to feed "line level" signals, below, through guitar effects.)

A guitar's output impedance might be a few tens of kΩ, whereas an effect's output is usually lower-impedance, like 10kΩ. The input is usually expected to be 1MΩ or more, in order not to lose signal or kill the tone. That extra-high input impedance for instrument-level signals is why some mixers, like the little Mackie I use, have a "hi-Z" option on certain inputs, meant for directly plugging in a guitar. Even though the regular microphone channels have plenty of voltage gain, they will not properly amplify an instrument-level signal because mic level is associated with much lower impedance.

Microphones and guitars are often passive devices with no built-in electronic amplification; the signal coming out of either is directly produced by capturing the energy of sound waves or moving strings, and that's why it carries so little power. When pieces of active electronic equipment are connected to each other, they have the luxury of transmitting much more power to each other, which helps overcome noise and interference. The level used for connecting powered equipment to other powered equipment in general, is called "line level"; and although there is more than one flavour of line level, it tends to be more consistent and standardized.

Consumer-grade audio electronic products with line level inputs or outputs, like "component stereo" devices, usually expect to transmit and receive signals at -10dBV, which is -7.8dBu and 316mV RMS. That is the level you will typically see on the red and white RCA phono jacks on the backs of devices - although the passive cartridges in actual phonographs, for which those connectors were invented, produce mic-level signals. These connections usually have low output impedance (less than 100Ω), and input impedance of 10kΩ or more.

Professional audio equipment, racked up in studios and typically using balanced XLR connectors, uses a "line level" of +4dBu, and of all the levels on the list this is the one that comes closest to being commonly and officially standardized. This level is equivalent to 1.228V RMS. Let me emphasize that it is the RMS voltage that is standard and predictable. There is not a standard "voltage range" for line level signals! When comparing against the pros, it's necessary to use the measurements they use. The input and output impedance for pro line level is, nowadays, usually similar to that of consumer line level. In former times, professional audio gear was often designed to use 600Ω for both inputs and outputs.

Some devices intended for a "pro-sumer" market use a line level of 0dBu; and such devices can reasonably be interfaced with both of the other line levels by turning the volume up or down a little on either end of the connection.

The highest level you're likely to see in common audio use is "speaker level" - the level of signal that directly drives the speakers. Here the signal is not just a signal, conveying information, but also a source of electrical power for producing a physical effect, so it needs to be much stronger. A common speaker level might be 0dBW, where W is for "Watt": this is the level that supplies 1W of power into the speaker's impedance, which is often 8Ω. Assuming 8Ω, 1W of power would be 2.83V RMS, or +11.2dBu; but, again, speaker level varies a lot depending on the size of the speakers and how loud you want them to be. In a big PA installation it could be very high.

Something like the headphone jack of an iPod is still theoretically "speaker level" because designed to drive (very small) speakers; but its actual voltage might be closer to that of line level, and that does mean you can plug it into a line-level input with a much higher impedance than a speaker. The high input impedance will just mean the input consumes much less power than the output was willing to provide.

Now, what about Eurorack signal levels? Precisely describing this is problematic because they are usually defined not by RMS but peak to peak voltage, and as we've seen, the crest factor is different for different signals and that makes a difference for the conversion between these two descriptions.

Doepfer's Technical Details A-100 Web page is the nearest thing to an official standard for Eurorack signal levels, even if many manufacturers (including North Coast) don't follow what it says about control voltage levels. For audio, it says levels "are typically" (underlining theirs) ±5V when the signal leaves a sound source such as an oscillator. I think most Eurorack manufacturers do follow that. My own products, like the Middle Path VCO, usually aim for ±5V as the approximate minimum output level given component tolerances. In practice there will be some variation and an output may really end up being more like ±5.5V. I figure it is easier to attenuate than to amplify, in a typical rack, and level differences of that magnitude are insignificant anyway.

Doepfer's wording implies, though I think many Eurorack users miss this, that the audio level may vary significantly at later stages in a patch as signals are filtered and mixed; my impression is that nonetheless, manufacturers assume the audio level always covers about a ±5V range with probably a few volts of headroom on either side. In practice, in a rack with a variety of modules, clipping will set in pretty soon if you try to run Eurorack signals much outside the ±5V range; there just isn't much headroom in Eurorack. I have seen some users try to demand a ±10V clipping range and I think that's unrealistic on a ±12V power supply; ±8V is more reasonable as a general expectation.

The output impedance level for Eurorack varies: it is often close to zero because of "in-the-loop" output resistors, but the nature of those resistors is to limit the available power output, so the modules set up that way will only really have low output impedance when driving typical Eurorack inputs with impedance in the 100kΩ range. In other words, you may not be able to use them to drive speakers even if these voltage and impedance specifications might seem like they should be able to drive speakers. Also, many modules don't use in-the-loop resistors and instead expose an output impedance more like 1kΩ, sometimes as part of an effort to allow output mixing through a passive multiple; and some "passive" modules have output impedance much higher, into the tens of kΩ. Eurorack input impedance is typically 100kΩ but that also varies in both directions.

All these Eurorack levels are, unfortunately, described in terms of "voltage range," and there is no simple conversion between that and RMS voltage or dBu. It all depends on the crest factor. A ±5V sine wave, with crest factor 1.414, is 3.34V RMS and +13.2dBu. A ±5V sawtooth wave with crest factor 1.732 is 2.89V RMS and +11.4dBu. More complicated signals will often tend to have higher crest factors and therefore lower RMS voltages and dBu levels when adjusted to ±5V peaks. My somewhat arbitrary estimate of 1% clipping on a normal distribution for program material, equivalent to a crest factor of 2.8, would translate to 2.30V RMS and +7.2dBu.

If we're going to be precious about "voltage drop," then maybe we should also subtract a further 0.087dB from each of the Eurorack levels to account for the difference between open-circuit voltage and a 1kΩ output impedance driving a 100kΩ input. But it's not usually meaningful to describe signal levels at that level of precision, and whether that "drop" even happens depends on the individual module's output circuit design.

At least we can say that for any fixed waveform and therefore crest factor, a ±8V range (which I think will safely pass through most Eurorack modules) is 4dB above a ±5V range, so we have about that much headroom in Eurorack. And we can get a rough idea of the amount of attenuation or boosting needed to get between other levels and Eurorack levels. With Eurorack at let's say about +10dBu, the translation to "pro" line level is -6dB (just cutting voltage in half); to "consumer" line level it's about -18dB; to instrument level assuming that is about -16dBu, the difference in level is -26dB; and to mic level the difference is anywhere from -50dB to -70dB.

Pro or even consumer line level is close enough to Eurorack level that if you want to connect them you can probably get away with just running a cable, turning down the volume on the Eurorack module, and turning it up on the other piece of equipment. That's why I tell people you probably shouldn't be quick to buy an "output" module. You don't need to spend the money and space on a special device that just does the equivalent of turning down the volume knob a bit. But if you're trying to interface to guitar effects and they really want instrument level and not line level, then you will probably need a fixed attenuator or "pad" to knock the signal down further than typical Eurorack adjustable attenuators can reliably go, and an amplifier in the other direction. Going reliably between Eurorack and mic level may require more than one stage of attenuation and amplification to do it well. If you want to drive a speaker or pair of headphones, Eurorack offers plenty of voltage but usually at the wrong impedance, so unless it's a very small speaker or pair of earbuds, you will probably need a speaker amplifier.

Here's a summary of these different levels. There are assumptions built into this table, including an effective crest factor of 2.8 for program material; the table shouldn't be taken as the last word on signal levels all by itself.

level	dBu	RMS	peaks	outputs	inputs
mic	-60dBu to -38dBu	775µV to 10mV	±2.2mV to ±28mV	~150Ω	1kΩ to 2kΩ
instrument	-20dBu to -14dBu	80mV to 160mV	±225mV to ±450mV	10kΩ (effect) to 50kΩ (guitar)	1MΩ
consumer line	-7.8dBu (-10dBV)	316mV	±885mV	<100Ω	≥10kΩ
pro line	+4dBu	1.228V	±3.44V	<100Ω or 600Ω (old)	≥10kΩ or 600Ω (old)
Eurorack (program)	+7.2dBu	2.30V	±5V	0 or 1kΩ	~100kΩ
Eurorack (sawtooth)	+11.4dBu	2.89V	±5V	0 or 1kΩ	~100kΩ
Eurorack (sine)	+13.2dBu	3.34V	±5V	0 or 1kΩ	~100kΩ
speaker	+11dBu or more	2.83V or more	±7.92V or more	8Ω (or 2Ω, 4Ω, 16Ω)	8Ω (or 2Ω, 4Ω, 16Ω)

Let me emphasize again that much of this is approximate and depends on assumptions. Really knowing which pieces of equipment will or will not play nicely with each other requires not only looking at the specific devices, but also the signals they will carry. Voltage range is usually the wrong way to understand signal levels; I've described RMS voltage, and impedance, which provide a better framework.

◀ PREV Power cycling and extra switches || It's the sales, silly! NEXT ▶