Fat sounds and thick pads
2021-09-08 MSK 013 MSK 007 music csound
From time to time we hear people claim that one synthesizer sounds more "fat" than another. For the sound to be fat is supposed to be a good thing. This is often cited as an advantage of analog synths over digital; or of one analog synth over another. Somehow it always seems to be the most expensive equipment that sounds fattest.
What does it really mean for a sound to be fat? Is "fat" just another word for "good"? In a blind A-B listening test, would you be able to pick out which of two otherwise identical sounds was the fat one? What besides analog electronics makes a sound fat? Is it true - as one manufacturer who shall remain nameless has claimed - that building a circuit with physically larger components can make it sound fatter? What about if you spell it "phat" - does that have the same meaning?
What's the synthesizer equivalent of Grove's Tasteless Chill Tonic (advertised above): the miracle cure that produces a really fat sound?
Ensembles are fat
I think it's clear that some people use "fat" arbitrarily, without any precisely definable meaning, for any sound they think is good. However, I think it's also sometimes used to describe something more specific that, in principle, could be objectively measured: a fat sound is the sound of an ensemble.
Record just one voice, or just one instrument, in a small acoustically dead room, with transparent low-distortion recording equipment. What you get is liable to sound "thin" - the opposite of fat. But if you record a choir, or a large string section, with many near-identical sound sources producing basically the same sounds all at once, and if you record in a larger room alive with reflections, then the result is likely to be what people mean when they say "fat." Instead of really having many instruments playing at once, you can use multitrack recording to stack up many takes of the same instruments on top of each other, and that's also likely to create a sound that will be considered fat.
If we take "fat" as meaning "having the characteristic sound of many closely similar sources playing in unison," then we can understand what features correspond to that in the spectrum, and figure out how to create those spectral features on demand.
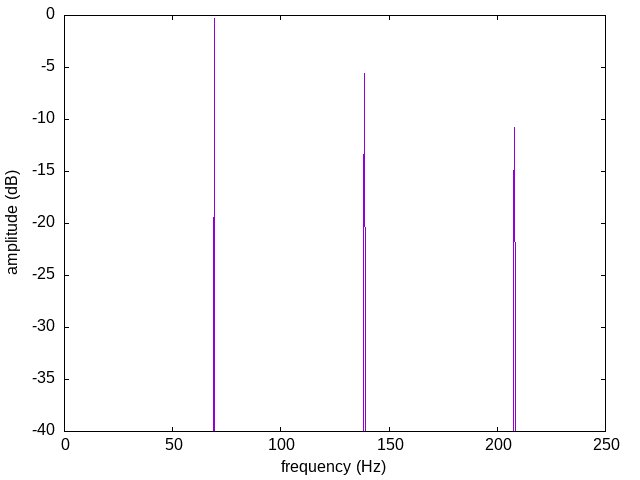
Fourier theory teaches that a repeating waveform - one in which each wave is exactly the same shape as the last - can be split up into a sum of sine waves at multiples of the basic repetition rate or fundamental frequency. Here's a spectrum of such a waveform. There are very sharp peaks at integer multiples of the fundamental, here 69.3 Hz (Db almost two octaves below Middle C - I chose this frequency because it's used in my audio examples later). This spectrum is what you might get from a very precise and stable oscillator playing a fixed, unchanging waveform without modulation.
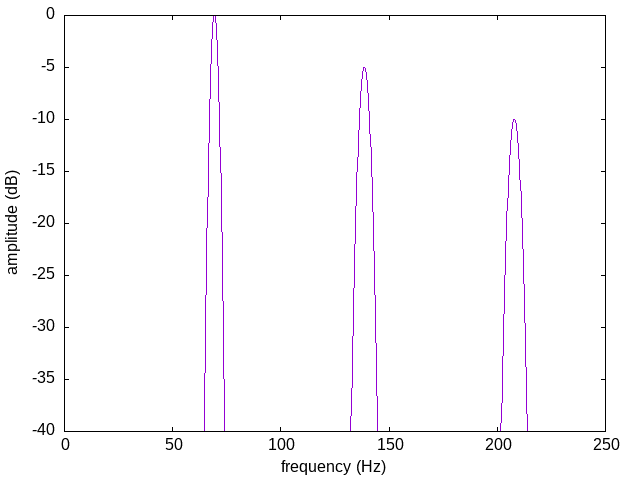
Suppose you take many such oscillators and mix the outputs. Assume each one plays a perfectly stable waveform, but they are not all synchronized or perfectly tuned to each other. Some of them will be a little higher-pitched, moving their spectral spikes a little to the right in the chart. Some will be a little lower-pitched, with spikes moved to the left. So instead of having sharp spikes in the overall spectrum at exact integer multiples of 69.3 Hz, you get a cluster of spikes that overlap to produce a wider bump, centred on each integer-multiple frequency. Each harmonic of the fundamental has spread out into a band.
It doesn't have to be electronic oscillators. Get a dozen violins playing in unison and the same thing happens. Each one produces a spiky harmonic spectrum, but they inevitably won't have identical tuning or timing, so instead of all hitting identical harmonics, around each harmonic of the consensus fundamental you get a little cloud of all the harmonics of the individual instruments. As a single sound, it's one made up of narrow bands centred on the harmonic frequencies, instead of spikes hitting those frequencies exactly.
That's a spectral characterization of fat sounds. Fat sounds are sounds in which the harmonics or partials of the spectrum have been spread out into wider bands. Thin sounds, in contrast, tend to have sharp spikes in their spectra.
The fattening modulation diet
Spread-out partials don't have to come from literally mixing together many perfectly stable signals with slightly different tuning. Modulation and instability can do the same thing to the spectrum of a single source. Take a sine wave, modulate it with another sine wave at a significantly lower frequency, and you end up with sidebands above and below the carrier. In the simplest case (balanced AM), the carrier and modulator themselves disappear and your two input sine waves are exactly replaced by two new ones at the sum and difference frequencies. Start with 100 Hz and 10 Hz input and you get 90 Hz and 110 Hz output. Other forms of modulation have slightly different spectral effects: unbalanced AM tends to allow some of the input signal through too, and angle modulation (frequency or phase - they are actually the same thing at this level) tends to create weaker additional sidebands separated from the carrier by multiples of the modulator frequency, depending on the depth of the modulation. But in all these cases of modulating a carrier with a lower-frequency modulator, the spikes in the carrier spectrum get spread out to cover wider bands, width scaled to the bandwidth of the modulator, making the sound fatter.
Modulation leading to fat sound is a clue to why analog electronics is thought to sound fatter than digital. If you've got an oscillator whose frequency is affected by temperature (and therefore air currents), power supply fluctuations, and so on, then those random factors cause the frequency to vary over the space of fractions of seconds to a few seconds. That's frequency modulation with an effective modulator frequency of a fraction of a Hz to a few Hz. The harmonics of the oscillator output get spread out into bands with width on that order of magnitude, creating the "fat sound" phenomenon. A digital oscillator deriving all its timing from a stable crystal would have less of this effect. Similarly, if you record an identical master tape onto a CD and a vinyl record and play them back, the mechanical instability of the vinyl turntable will add a little bit of phase modulation, spreading out the harmonics in a way that won't happen with the CD player, and someone listening may at least claim that the vinyl playback sounds fatter.
But - just as a gimmicky fad diet may help you gain weight but not necessarily keep it on - modulation of a thin input may not work as well for creating fatness as a real ensemble would. The human ear is very good at detecting and decoding correlations. If you take a single oscillator, which sounds thin because its harmonics are very pure tones at sharply defined frequencies, and you modulate it with a pure sine wave at a low frequency, the result doesn't sound like many oscillators playing together. It sounds like one oscillator, modulated! The listener's ears and brain are able to detect that the modulation of every harmonic is the same, and then they hear the carrier and modulator signals as separate entities. The listener hearing the vinyl record may perceive it as a thin recording played on an unstable turntable (which it is) rather than a fat recording.
Each harmonic in this situation may look like a nice little band on a spectrogram, but the fact that the modulation is correlated between harmonics allows human auditory perception to infer the simpler origin of where those bands came from. In order to fool the ear into perceiving a larger ensemble, we need to create a more complicated signal in which the modulation of different harmonics into wider bands, is not so obviously correlated.
It helps to use something more complicated than just a sine wave as the modulator. Then the structure of each harmonic band becomes more complicated, with more little spikes overlapping and less ability for the ear to break it down into simpler parts. In a modular synthesizer, we might achieve that by mixing several LFOs, or using filtered noise, to create the modulator signal. That doesn't address the correlation across different harmonics, though. Using multiple kinds of modulation at once can help, because it may be possible for them to affect different harmonics differently.
Reverse engineering a fat pad
Let's break down what's going on in an example of a fat sound, and then reconstruct it with different synthesis techniques.
I'm going to start with a clip from the intro to the song 星の生まれる日。 by Cocco (Hoshi no umareru hi, "The day a star is born"). The rest of the track isn't particularly relevant here, but you can find the whole recording on YouTube and my translation of the lyrics on my personal site.
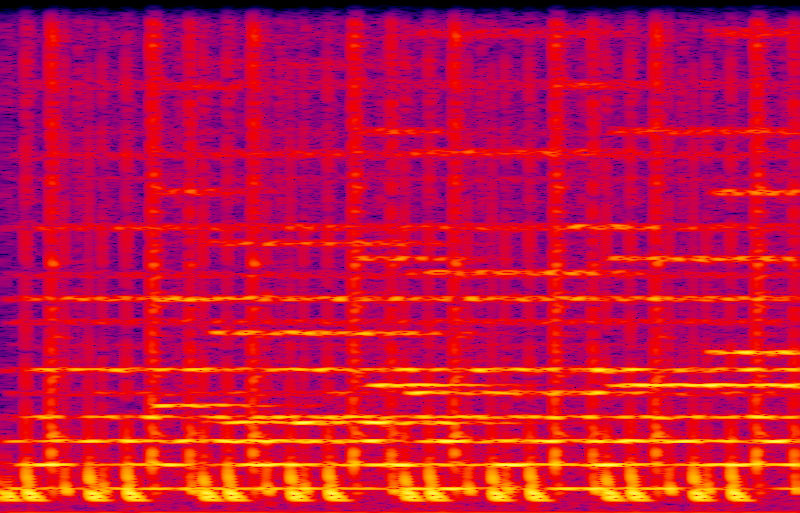
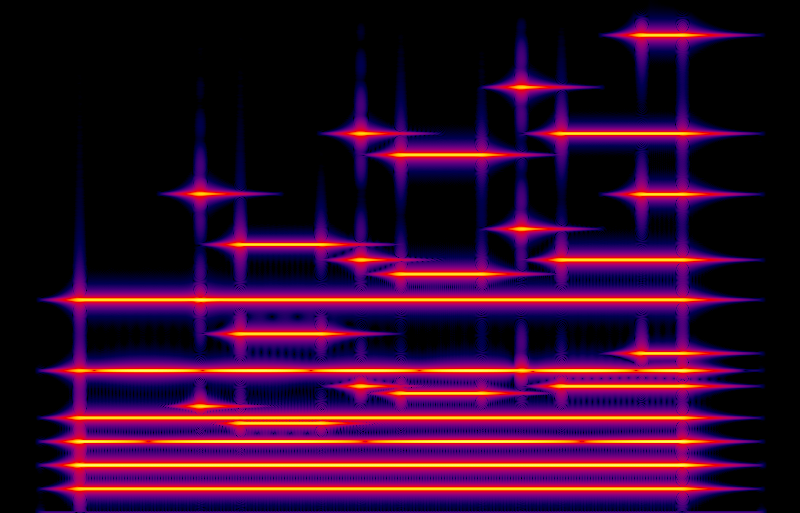
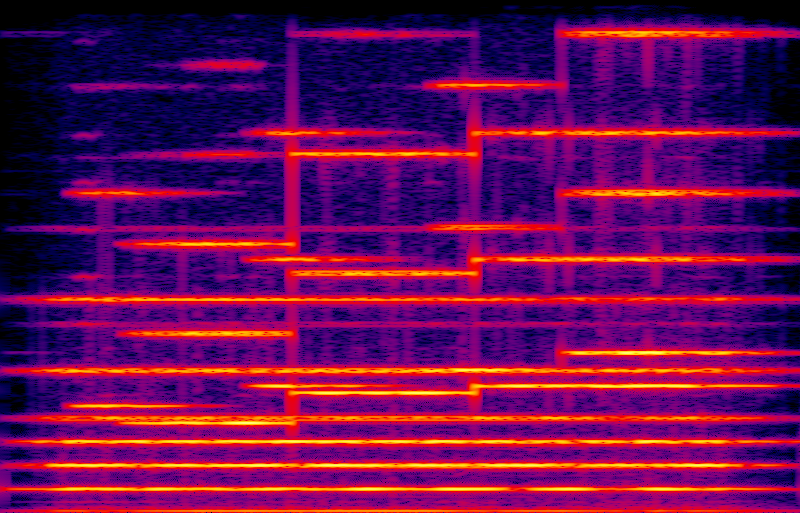
Now, here's a spectrogram of that clip. This image represents a collection of spectra, like the ones above, taken separately over small windows centred at each position in time through the clip. Time reads from left to right covering the length of the clip, increasing frequency reads from bottom to top covering 0 Hz to 1500 Hz, and the colour density represents amplitude.
The percussion track creates pulses of wideband noise-like sound in a repeating pattern; those are visible as vertical bars on the spectrogram. Ignoring the percussion, the other thing going on in this clip is a sort of ethereal, shifting, and dare I say it "fat" sound that will become the harmonic backdrop of the whole track once the vocals come in just after this clip. That kind of sound is usually called a synth pad. I don't know the exact original instrumentation used here, but given this was recorded in Japan circa 1997, it was quite likely a digital synthesizer from Roland, Yamaha, or similar. I really like synth pad sounds and have spent a fair bit of time chasing down different ways to create them.
Looking closely at the spectrogram and verifying it with point spectra taken in strategic places, we can determine that the pad sound in this clip is basically made up of the first, second, and third harmonics of each note; and those harmonics are spread into little bands, just like the other fat sounds discussed above. Through the whole clip there are three sustained notes, serving as what modular synthesizer users might call a "drone" and other musicians might call "pedal points." The pedal points are the Db almost two octaves below Middle C; the Db one octave up from that; and the Ab up a further fifth.
Here's my transcription of the notes in the clip, ignoring the percussion.
Visit these chords in the chord database: Dbsus2 Gbsus2+#4 Db Gb+2
The three pedal points line up with the first three harmonics of the low Db (69.3 Hz, 138.6 Hz, and 207.9 Hz - but note that equal temperament means the Ab is not actually played at exactly that frequency); so with the three harmonics of each note provided by the instrument, we're getting the first three harmonics of the first three harmonics, creating a pattern of harmonics numbered 1, 2, 3, 4, 6, and 9 for that single fundamental, some of those numbers being hit by more than one of the original notes. All this ties the entire clip tightly to the low Db at 69.3 Hz, which defines the key for the entire song.
You can see the harmonics of the Db pedal as bright horizontal bands across the entire spectrogram. Missing harmonics, like number 5, are visible too but much weaker - you can count across them to verify that numbers 1, 2, 3, 4, 6, and 9 are the strong ones. Note how the bands get wider near the top; and, especially near the bottom, they have a beaded appearance suggesting that some of the harmonics are appearing and disappearing over time (slow amplitude modulation). However, this apparent modulation is not synchronized between the different harmonics, and it's not in a repeating regular pattern. This clip does a good job of sounding like a real ensemble and not only a thin, modulated, single source.
Looking at the non-pedal notes, and the chord names I've added, we can see some of the musical features often associated with how people use pad sounds in tracks. There's a lot of emphasis on perfect fifths in the harmony. Most of the chords also contain major seconds (the major second is the fifth of the fifth). These harmonies tend to create a "sweet" sound to go with the poetic content of the lyrics - possibly sweet to an excessive degree, judging from some criticisms I've heard of this particular song, but that's not the main point to discuss today.
Also not my main point, but I wanted to mention it, that the pattern of using the first three harmonics of each note goes back a long way. It's basically the same thing you get by playing the common "88 8000 00" registration on a Hammond organ - and Hammond organ players also often use a device called a Leslie which mechanically adds amplitude and phase modulation that widen the harmonics into bands, fattening the sound. The digital synth in the 1990s was being used to create a type of sound that we can trace back to earlier pop and rock music just by looking at the spectrogram.
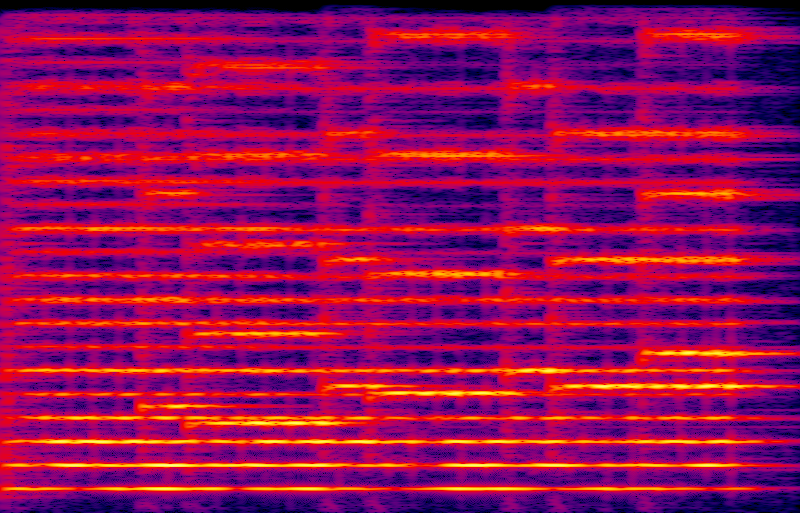
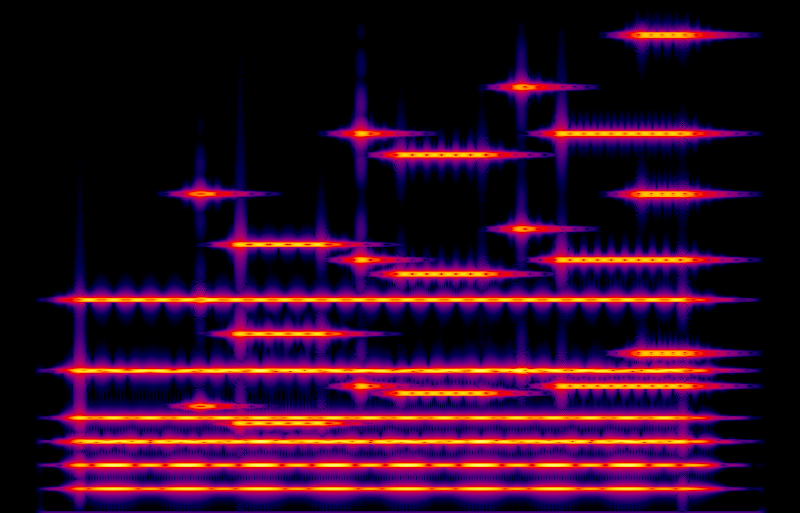
As a quick check of my transcription, without attempting to match the timbre, I've recorded my transcription on a Roland D-05 with the "Arco Strings" preset. This is a decent digital approximation of a large string ensemble. Comparing this spectrogram to the one from the Cocco track, this sample shows a broader selection of harmonics; a very similar widening of each harmonic into a band with the details of the bands independent of each other, making the sound "fat"; and some vertical percussion-like features which seem to come from the bowing.
Additive synthesis in Csound
Additive synthesis - actually generating each partial of the sound separately - is probably the ultimate technique for making fat sounds. But just like actually building a large ensemble, it can be expensive, especially in the analog realm. Let's explore what we can do digitally with Csound.
Csound is a sound generation and processing system controlled by its own language somewhat similar to assembly language. Although the interpeter is written in the C programming language, Csound's own language is not at all similar to C - that's a common misunderstanding. It's essentially a modular synthesizer realised as a programming language instead of a hardware device or graphical environment. Because Csound allows precisely specifying waveforms and processing operations, it's useful for testing ideas on synthesis techniques without the overhead of building hardware or writing code for a more general-purpose platform.
This article is not intended as a Csound tutorial and I'm not even going to quote the source code for my examples inline. My subject matter here is additive synthesis and making sounds fat, not the particular software synth that I'm using to perform those techniques. But you can download a ZIP file of the source code and take a look at the online Csound manual if you're interested.
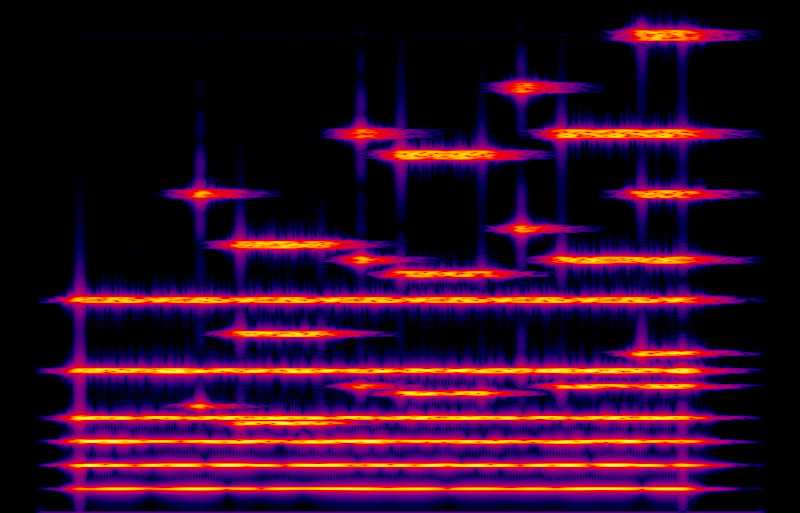
When taking apart the pad sound in my sample clip above, it seemed that the synth pad instrument was basically just playing harmonics 1, 2, and 3 for each note, with slow attacks and decays. So the simplest way to do that would be to run three sine-wave oscillators for each note, at exactly the harmonic frequencies for the note, and fade them in and out with an ASR envelope. Here's a recording of that, and its spectrogram.
I think the recording is recognizable as the same notes, but it sounds thin. It's a very static sound without motion in it. We can see in the spectrogram that the signals are very pure - the black background indicates that except for transient effects caused by the attacks and decays, there is basically no stray noise at any frequencies except the harmonics I deliberately created. The lack of noise is understandable because this sound file was calculated, not really recorded - to the extent the file formats permit, there is really nothing there except the sine waves I described.
But even though these are just pure sine waves, there is still something that sounds like modulation. Some of that (visible as interruptions in the horizontal lines for the third and sixth harmonics) comes from the 0.3 Hz discrepancy between the fundamental of the equally-tempered Ab and the true third harmonic of the low Db. But I think most of the audible pseudo-modulation in this recording is from the higher notes, shown on the treble clef, beating against nearby harmonics of the pedal points. You can see that where the shorter horizontal lines on the spectrogram come close to the grid of pedal harmonics; two sine waves close together will be heard as one with AM at a rate corresponding to the frequency gap between them. If the pedal sound were fatter, then the ear might be less likely to interpret these beat frequencies as harsh, intrusive modulation.
Let's try to make this sound fatter. Here's a version in which each of the sine waves (three for each note already, to hit harmonics 1, 2, and 3) is replaced with a cluster of three sines, at 99%, 100%, and 101% of the straightforward harmonic frequencies. So, according to the general recipe for a fat sound, we're widening each harmonic into a little band covering more of the spectrum.
I think that does sound better and fatter than the one sine per harmonic version. The beat frequencies between distinct notes, such as in the final chord, have pretty much gone away. However, it still has some features both visible and audible that make it seem like an artificial construction and not so much like a real ensemble. You can see a regular repeating pattern in each horizontal band of the spectrogram. We've replaced each sine wave from the previous example with three, at close equal spacing; but the ear tends to perceive such a set of three sine waves as a single wave with amplitude modulation. The AM in different harmonics of the same note is also synchronized, further increasing the tendency of the ear to decode it. And that is audible in the recording: the ear picks up a regular pulse at a rate of a few Hz in each of the melody notes. Real ensembles don't sound like that.
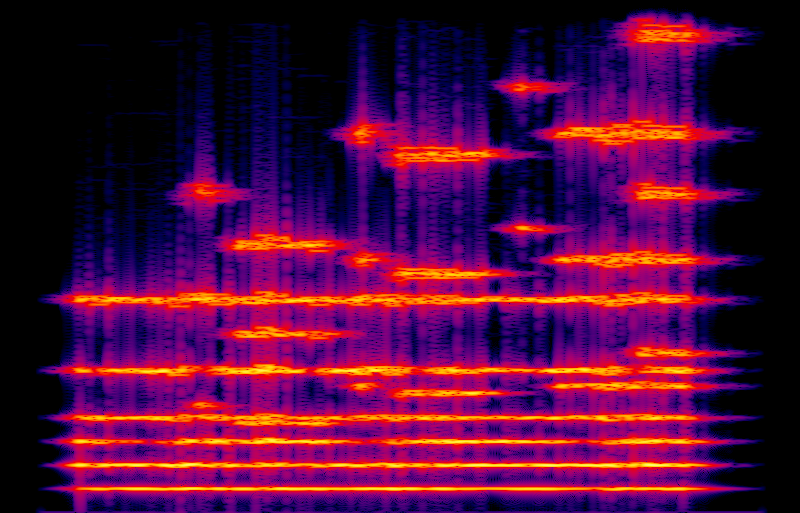
Using three close-together sines isn't really enough to create a solid band in the spectrum; the listener still picks up the spiky structure within each band. So, let's use more sines. In this next example I'm using a bank of 21 sines for each partial, uniformly spread from 99% to 101% of the centre frequency (that is, at intervals of 0.1%). I'm also starting them all at random phases instead of all at zero like the previous examples; and I'm using a separate set of sines each for the left and right channels, to get some stereo. Here's the result.
That sounds a lot better, and a lot fatter. Using so many sines so close together, with random phases, means that the frequency of each partial is basically wandering unpredictably within the designated band. That's visible on the spectrogram as non-repeating, roughly random colour effects within the horizontal features. Also importantly, the modulation or wandering is independent in each partial, and (not shown on the monophonic spectrogram) independent between left and right. The resulting spectrum is very close to what a listener would encounter in real life when sitting in the middle of a large ensemble of closely similar instruments all independently tuned close but not perfectly to the same pitch.
However, this is an expensive form of synthesis. I'm computing 126 independent sine waves (3 partials times 21 sines per partial times 2 channels) for every note. It doesn't take very long on a fast desktop PC but it's a lot to ask of something like a synthesizer module, which probably has less computing power. Can we get a similar effect at lower cost?
Here's an idea: let's start with pure sine harmonics and then try to add the spectral broadening all in one go after the fact. That is basically what a chorus effect does. We'll take multiple copies of the pure-sine signal, cause them to sound just a little different from each other somehow, and then mix them back together. Instant ensemble.
I built a simple chorus effect in Csound, typical of the real ones people use. It runs each channel into a delay line with five taps on each delay line. Each tap varies between 3ms and 17ms delay time, varying slowly according to a smoothed random number sequence at a rate of between 0.5 Hz and 3.0 Hz. When the delay time is decreasing, the pitch of the signal coming out of the tap is shifted up a little; when the delay time is increasing, the pitch is shifted down. So at any given moment, for each channel we have five versions of the signal with small random pitch shifts, and these pitch shifts are constantly changing. That means every sine-wave component in the input to the chorus gets split into a little cloud covering a band centred on its original frequency. Here is the spectrogram and the audio.
I think it's fatter than the pure-sine version; but it's not as good as the version with 21 independent sines per partial. One thing quite visible in the spectrogram is the correlation between different partials; especially near the upper right of the spectrogram, the random pattern created by the spectral spreading is the same in different bands. In the audio, that corresponds to the listener being able to hear the movement of the delay taps. To some extent this sounds like a smaller ensemble moving around rather than simply a larger ensemble. But it's doable with less CPU power, and the cost of running the effect does not increase as we add more notes to its input. This approach can fatten up the entire signal all at once. That may be a good trade-off.
Fat pads with analog Eurorack
It's probably not realistic to use 126 sine oscillators per note if we are patching real analog hardware; only "Look Mum No Computer" builds synthesizers that way. So it may be better to reserve the bank-of-sines approach for software. In analog hardware, we'll need to find a different approach. As discussed above, an oscillator repeating the same unchanging waveform gives a spectrum consisting of narrow spikes at integer multiples of the repetition rate. We can spread them out into bands to create a fat sound by modulating the oscillator; but modulating all the partials at once with the same modulator gives a result that may not sound realistic. The tricky bit is keeping the modulation of the different partials uncorrelated, without needing too much additional hardware.
One easy trick for a fat sound in analog synthesis comes from the following observation about sawtooth waves. Suppose you've got two sawtooths of the same frequency and amplitude, one of them rising and the other falling. Most of the time, one of them is rising and the other is falling at the same rate; so if you add them together, the sum is a constant. But every so often, one of them will reset, causing the sum to jump up or down. With the two saws at exactly the same frequency, they just take turns resetting, and the sum is a pulse wave.
Now, think about the pulse width. I've shown the sawtooths 90° apart, and they give a 50% pulse width when combined. One sawtooth creates the rising edge, the other creates the falling edge, and they can move independently. If one sawtooth's phase moves a little earlier or later relative to the other's, then the pulse width grows or shrinks. If one sawtooth is a slightly higher or lower frequency than the other, that is the same as steadily pushing the phase forward or backward, modulating the pulse width steadily between 0% and 100%, then wrapping around, as if by another lower-frequency sawtooth. The important insight here is that a pulse wave is equivalent to two sawtooth waves in unison, and the main effect of modulating the pulse width is to modulate the relative phase of the two component saws.
In any patch where we would use a sawtooth wave, we can substitute a pulse wave with modulation of the width, and get the effect of two sawtooth waves in unison. It only works well across a limited range of depths and modulation frequencies, but even just a single-oscillator patch sounds a lot fatter with this modification.
To take it further, we can use multiple oscillators. Here's a sketch of a patch I built with two Middle Path VCOs, each of which contains two oscillators. With width-modulated pulse waves, that comes to eight sawtooths in unison.
The pitch CV from the MIDI interface goes through a buffered multiple to drive the V/oct inputs of the two Middle Paths, and the two Leapfrog VCFs. The oscillators are all tuned to the MIDI pitch, in unison - but being analog, their tracking will never be quite perfect, so they will be very close to each other but not quite at identical frequencies.
Four low-frequency sines from the Fixed Sine Bank are patched into the four PWM inputs of the oscillators. Then the pulse outputs are patched (with very short cables) to the corresponding inputs of the shaper section on each Middle Path.
The Middle Path's shaper section is not at its best with pulse-wave inputs because it is voltage-based. Put in a single pulse wave and all that comes out is another pulse wave, possibly with a different amplitude and some DC offset. But it's another story when there are two pulse waves as inputs to the same shaper. I also ran two more sines from the Fixed Sine Bank to the middle inputs of the Middle Path shapers, to create even more motion in the spectrum. The shaper acts as a nonlinear mixer. The frequency components of the inputs, which in this case are all narrow bands centred on the harmonics of the one note both oscillators are playing, will interfere with each other and spread out a little more, each output partial picking up a different pattern of modulation according to which input partials add and subtract to line up with it. That gives the uncorrelated modulation of different partials that we want for a really fat ensemble sound. As a bonus, each shaper has a pair of outputs with substantially the same spectrum but different per-partial phase: the sin and cos outputs. Those work well as "left" and "right" to create a stereo image.
I mixed the sin outputs from both oscillator modules, and the cos outputs from both, to create left and right signals. Two Transistor Mixers are shown in the patch diagram, although I actually only had one in my rack when I patched this and ended up having to use another manufacturer's product for one of the channels. Using the AC output on the Transistor Mixer helps remove DC and LFO feed-through.
The mixer outputs are something like super-saws: spectra consisting of bands of complicated modulation centred on each harmonic of the note from the MIDI interface, going up to fairly high harmonics. To replicate something like the spectrum of the pad sound we were going for in the software-synthesis part of this article, we want to cut off everything beyond the third harmonic; and the Leapfrog VCF, with its precise tracking and very sharp cutoff, is ideal for that. I'm using one for each of the two stereo channels - and using the filters' built-in VCAs, driven by a multed envelope from a Transistor ADSR on the slowest speed range, to create the smooth, slow attacks and decays associated with pad notes. The amplitude coming out of the oscillator shapers is high, variable, and not easy to control, so I turn the knobs on the mixer down a fair bit from their maximum to reduce distortion resulting from overdriving the filters. Even so, there's some distortion at the highest peaks.
I recorded five tracks: one for each of the three drone or pedal notes, and two tracks for alternating notes in the treble, to allow a long decay time after each note before the next one starts. Here's the result of mixing down those tracks on the computer.
I think it comes pretty close to the fat pads I was making with Csound, and the patch is a good fit to what works in analog. You can see from the spectrogram that it is decently close to the same spectrum as the software-generated tracks. You can also see vertical bars, indicating wideband transients, whenever a new note cuts off an old note in the same voice. That came about because the decay tails of my notes are, in some cases, longer than the time between notes. The transients are a little bit audible when listening to the recording. I might have avoided them by splitting my notes across even more separate tracks, to allow even more space for the tails. Shortening the tails and then using a reverb of some kind to stretch them out might also be a good option.
This patch uses several expensive modules just to record a single note at a time, and five-way multitracking when I'm trying to make things sound "fat" might be seen as cheating in some way. Of course it'll be fat if I combine five recordings, right? But it's a fact that the pros cheat. If at the end of the day I'm able to make the sound I want with the equipment I have, I'll do it with whatever techniques are necessary to get the job done. Few to none of your favourite albums were recorded by engineers who took vows of chastity to not record with the techniques that worked. And, of course, if someone wants to buy five sets of the modules above (a few tens of thousands of dollars' worth of equipment) in order to record five voices of this patch all at once with no multitracking and no "cheating," I'll be happy to sell them that and may even offer a quantity discount.
If I didn't happen to have two Middle Paths and two Leapfrogs on hand, I could get the equivalent of four sawtooths, still a pretty fat sound, with just one Middle Path. Even half a Middle Path - just a single pulse wave with width modulation - can give a decent ensemble sound when the modulator is something like a mixture of two or three low-frequency sines. Independently of the oscillators, I could cut down to one Leapfrog in this patch by sacrificing the simultaneous stereo output.
The better reason to avoid multitracking is to be able to perform the sound in a live context, and I did some other patching experiments aimed at playing all the voices in a single patch for that purpose, using one oscillator section for each voice, dropping the higher of the two Db notes in the drone to bring the total down to four, and feeding different notes through the same shapers at the same time. I also tried cross-patching the shapers on two Middle Paths, with the "both" output from each one plugged into the middle input of the other. The results of those experiments were interesting, certainly fat, and they might be worth using in some future projects, but they also indiscriminately hit all harmonics instead of giving the more specific complicated structure I was trying for. The Leapfrog with its sharp cutoff cannot really be tuned to include the ninth harmonic without also including the seventh and eighth, and that makes it hard to get the drone sound as I wanted it. It always seemed to end up either as bright as I wanted, but too gritty from the intermediate harmonics; or nice and smooth but too dark because of leaving out the high harmonics.
When I included a treble note along with any other note (drone or even just the decay tail of another treble note) in the inputs to any one shaper, I got a lot of intermodulation between the different notes and ended up with inharmonic partials I didn't like. So I think running the notes through the filters separately and combining them downstream of the filters is really necessary to get a close match to the strict three harmonics per note timbre that I was aiming for this time; and that implies either multitracking, or using a lot of filters.
To conclude: I've described what I think "fat" actually means in the context of synthesizer sounds, and how to create pad sounds with that attribute in a software additive synthesis environment. I've also made an attempt at achieving the same effect by patching a modular synthesizer. Some of these experiments work better than others, but even the ones that don't work well provide some insight into how sounds come to be called "fat."
◀ PREV Gracious Host development adventures || A stripboard Eurorack power cable tester NEXT ▶