Equivalent circuits
2022-08-06 electronics design
Thinking in terms of equivalent circuits is one of the basic mental skills needed for understanding electronics. I use the concept of an equivalent circuit implicitly in a lot of my writing about other things, but it's probably worth stepping back and learning about equivalent circuits in themselves.
An equivalent circuit is an as if circuit. If we're looking at a complicated circuit with behaviour that may be difficult to analyse, quite often we can say that (at least within a limited scope) the complicated circuit behaves as if it were really a much simpler circuit, the equivalent circuit. Then we can use that simpler equivalent as a substitute for the real, more complicated, circuit when looking at how it interacts with other things.
In modular we hear a lot about "impedance," but the consequences of impedance and what that word refers to often seem mysterious, and most wigglers don't have a clear understanding of how it affects connections between modules beyond the facts that sometimes, it does affect the connections, and that that can be a problem. Impedance is simply the resistance that appears in some kinds of equivalent circuit, and treating all the inputs and outputs as if they were replaced by their equivalent circuits with the appropriate impedance values, makes it relatively easy to figure out what happens when inputs and outputs get connected together. Similarly, equivalent circuits make it easier to understand how power supplies and modules interact - another topic that feels like a mysterious black art to users who haven't learned how to use equivalent circuits.
As a warm-up, consider the way resistors and other components can be connected in series and parallel to get new values. If you put a 27kΩ and a 68kΩ resistor in parallel, the combination behaves as if it were a single resistor with a value of about 19.3kΩ (subject to tolerance).
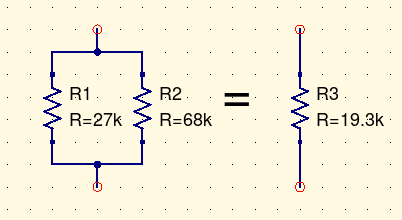
If you attach an ohmmeter to the two terminals of the parallel combination, it reads 19.3kΩ. If you apply a voltage and measure the current, you find that the current is 1/19300 amperes per applied volt. That is what a 19.3kΩ resistor does; in some sense you have a 19.3kΩ resistor right there. But if someone asks you to point out where the 19.3kΩ resistor is, all you can do is indicate the two resistors you actually built and say, well, these two resistors of other values together are equivalent to one resistor of the indicated value.
That idea of applying a voltage and measuring the current is key to how we can derive useful equivalent circuits: the equivalent circuit is the one that, at least within the scope of what we're trying to do with it, will have the same response to applied voltages and currents as the "real" more complicated circuit.
Thévenin equivalents
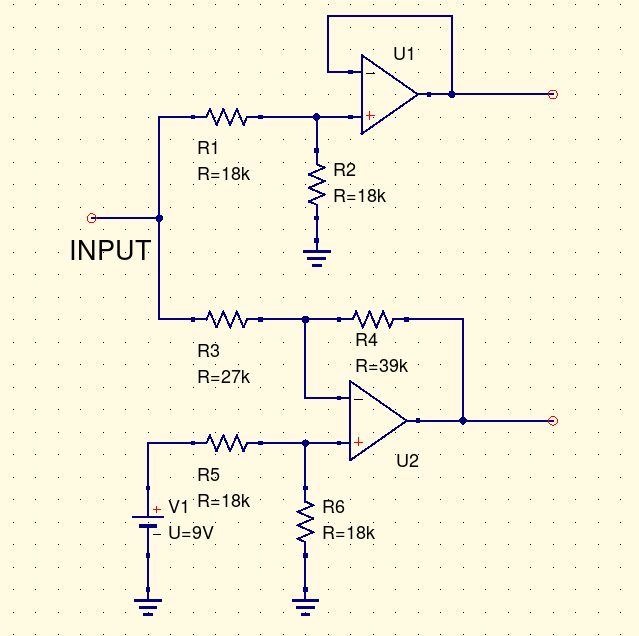
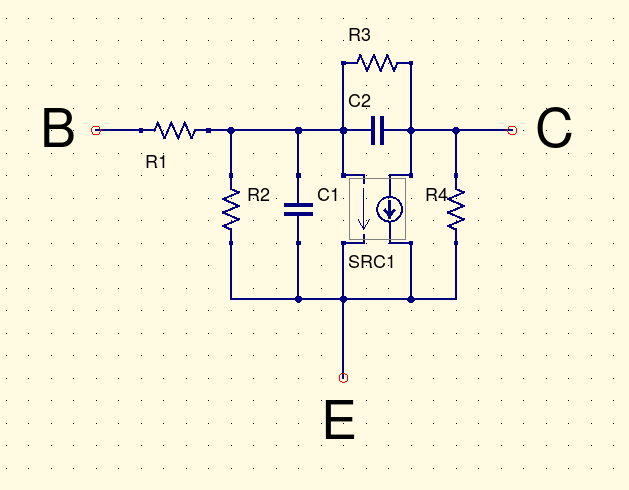
In this circuit a single input is driving two op amps, one inverting and one non-inverting. Suppose we're trying to understand what kind of load this circuit will place on whatever we connect to its input.
Even if we think we understand an inverting op amp circuit, and a non-inverting op amp circuit, separately from each other, it's not at all obvious what happens when they're connected in parallel. Do they interact in some strange way? Can we combine them like the parallel resistances above, by some simple formula, into a simpler equivalent circuit that still expresses what's important about this input circuit in terms of interacting with the things we attach to it? Or is a combination of two amplifiers just irreducibly complicated?
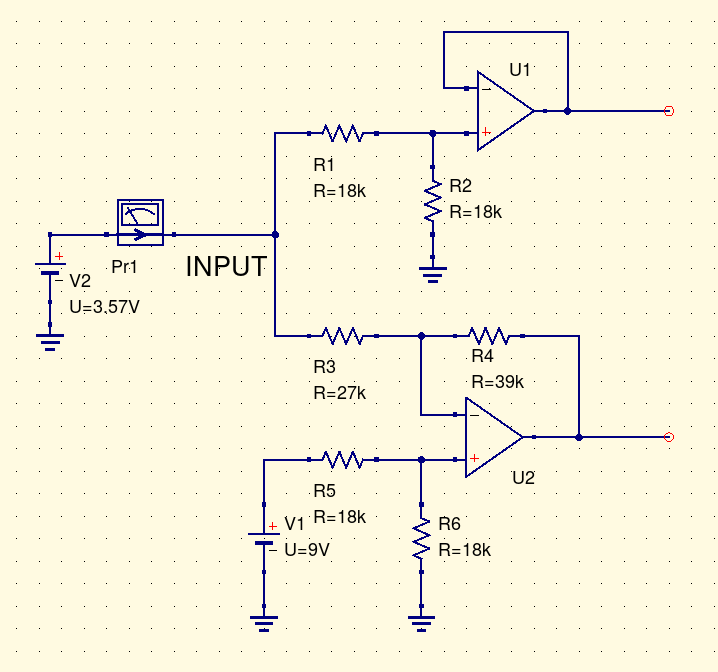
As a first step, just suppose we connect nothing to the input except a theoretically ideal voltmeter, and measure the open-circuit voltage. We could actually build it and measure; measure in a circuit simulator like Qucs, the one I'm using for my screenshots; or try to calculate it as follows.
As described in one minute op amp analysis, an op amp in negative feedback will try to bring its negative input equal to its positive input. The voltage divider of R5 and R6 holds the positive input of U2 at 4.5V. Then that's the voltage at the negative input as well. A chain of resistors (R3, R1, R2) connects that 4.5V node to ground at 0V, with nothing else to affect the voltages. So we can do a voltage-divider calculation: the total resistance along the chain is 63kΩ, dropping 4.5V, that is 14kΩ per V (which happens to be the inverse of the current passing through the chain: 71.4µA), the input is 36kΩ up from ground, so it is at 36kΩ/(14kΩ/V) = 2.57V. Hitting F8 in Qucs to "calculate DC bias" may be easier than doing that hand calculation, and gives the same result, 2.57V at the input node.
If instead of leaving the input open, we attached a regulated power supply with a voltage of 2.57V, it would have very little effect: no current would flow into or out of the input because that's just the voltage the circuit is trying to keep on that node anyway. But what if we tried to raise the voltage one volt, with an external power supply set to 3.57V? Let's also include a current probe (simulation equivalent of an ammeter).
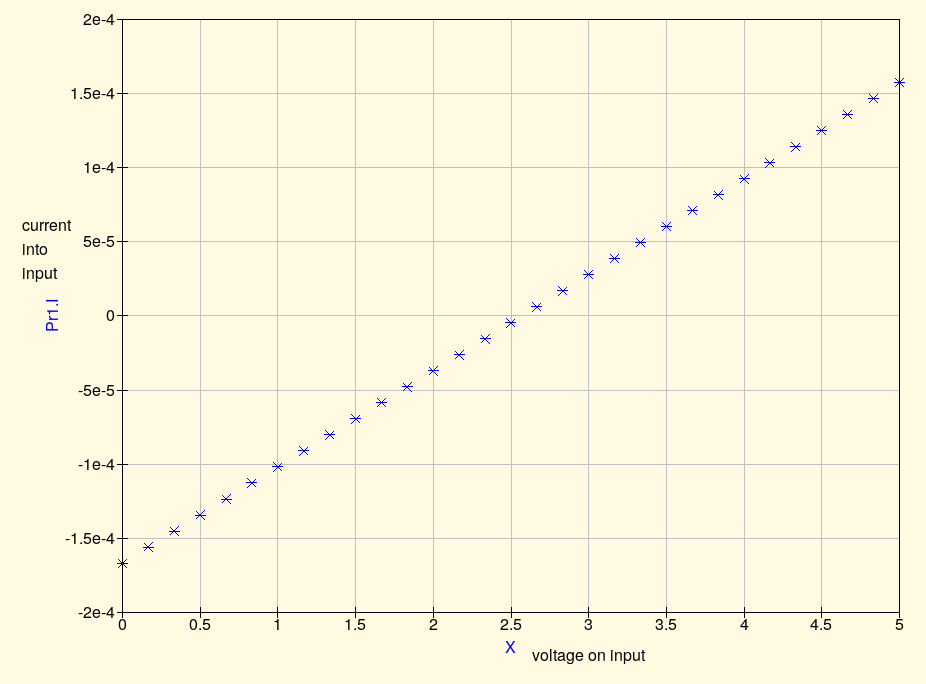
Simulating this situation (with more precision than the rounded figures I'm writing in this text) gives the result that it takes 64.8µA of current flowing into the input, to raise the voltage one volt. Now, here's an interesting thing: if we try instead to lower the voltage, with a regulated 1.57V voltage source, it turns out that we get 64.8µA flowing out of the input. It's equal and opposite. That's a clue: there is a very simple relationship between voltage and current. No current flows when the input is at 2.57V, and at other voltages, current flows in or out according to the difference from that voltage, at a rate of 64.8µA per volt we push or pull it away from 2.57V. The simulator can plot a nice little graph of the current into the input according to the imposed voltage. This linear behaviour would break down if the voltages got far enough from the centre to drive the op amps into other modes (such as clipping), but it works over the range shown.
There's a name for a thing that pulls 64.8µA of current per volt. It's called a 15.4kΩ resistor. Within certain limits, which include sticking to voltages that don't cause other behaviour from the op amps, what we have here isn't really an elaborate op amp circuit; it's really just a fancy way of building a 15.4kΩ resistor in series with a 2.57V voltage source. And that is an equivalent circuit for the double op amp input. Simulating this equivalent circuit gives the same current to voltage curve as the original two-op-amp circuit.
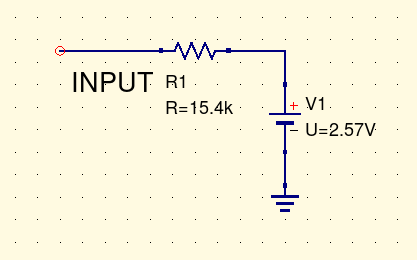
This kind of equivalent circuit, consisting of a resistor in series with a voltage source, is called a Thévenin equivalent circuit, and the mathematical result describing the frequently-occurring conditions under which it is valid to construct them is Thévenin's Theorem, both after Léon Charles Thévenin, of the French telegraph agency, who proved the theorem in 1883. Hermann von Helmholtz independently derived the same result in 1852.
The value of the voltage source in the Thévenin equivalent circuit is always the open-circuit voltage of the circuit. The resistor value is what we call the impedance of the circuit, and it's very important in understanding how this circuit will interact with others. Impedance might be measured as above by trying to raise or lower the voltage one volt at a time and measuring the current flow; or (if the open-circuit voltage is not zero, and the circuit can tolerate this condition while remaining in normal operation) by measuring the current the circuit will drive through a short circuit. We could measure it in a real circuit, or try to calculate it by simulation or other techniques. In the example circuit, we could get the input impedance by knowing that the input impedances of the two op amp sections are 36kΩ (series combination of R1 and R2) for the non-inverting section and 27kΩ (R3) for the inverting section; these combine in parallel to give 15.4kΩ.
That calculation already gives a clue to what we can do with Thévenin equivalents: we can find the equivalent for a larger circuit by first finding the equivalent circuits for smaller sections and then combining them. The resistances end up in parallel, and the open-circuit voltages work out according to a voltage divider calculation.
It's important to remember the difference between the impedance in the equivalent circuit, which we might denote by a resistor symbol on a diagram, and a literal resistor physically built into a circuit. Sometimes, like at the input of a typical inverting op amp circuit, there may be a single real component that corresponds exactly to the impedance. But quite often there is no single component corresponding to the impedance. Impedance may be a resistance without a resistor.
Equivalent circuits are as if circuits. There may or may not really be a resistor in series with the circuit, and if there is, it may or may not have a value equal to the impedance; but the Thévenin equivalent circuit says that the circuit behaves as if it consisted of a voltage source in series with a resistance, and the impedance is by definition the value of that as-if resistance.
Impedance also may not really be a resistance. In an AC situation it may include a reactance, that is a capacitive or inductive component, in addition to or instead of the resistive component. The math works out correctly if you just substitute complex numbers throughout the calculations, but it often is not really as simple as that because reactance is usually frequency-dependent and a pure Thévenin equivalent circuit may end up only being correct at a specific, fixed frequency. I'll talk a little bit more about AC and more complicated equivalent circuits below, but the simplest thing to remember is just to be aware that whatever equivalent you are using may be limited in its scope: it may only be valid at certain voltages, at a fixed frequency, as long as other components remain in a specific operating mode, or for some but not all analytic purposes.
If there were really a simpler circuit that could substitute for yours in all cases, then you would build that one instead of the more complicated circuit in the first place, and it wouldn't be just an hypothetical "equivalent."
The consequences of impedance
Knowing the impedances of inputs and outputs is useful in predicting how they will behave when connected. Here are two Thévenin equivalent circuits connected to each other. Maybe the one on the left is an output and the one on the right is an input, so the output is driving the input; but I deliberately haven't marked them as such, nor specified the values. The same circuit could describe an output patched into another output; or maybe a power supply providing power to a module.
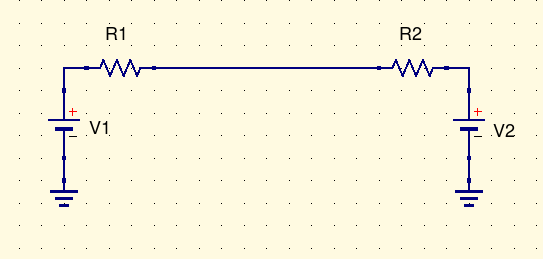
If one of the impedances is very small compared to the other, then the voltage in the middle will be basically equal to the voltage on the small-impedance side. That is usually the situation with Eurorack outputs driving Eurorack inputs: the target is for output impedance to be "small" (often effectively zero, with in-the-loop op amp output resistors), and for input impedance to be "large," often 100kΩ or more. Setting R1 to zero and R2 non-zero makes the middle voltage equal to V1: if V1 is the output, then the voltage where they connect has no "droop."
Some module outputs have more output impedance, like maybe 1kΩ. If we set R1=1kΩ and R2=100kΩ then the voltage in the middle will be a weighted average, 100 parts V1 and 1 part V2. The open-circuit voltage of module input circuits is often, not always, zero, so in this situation the voltage where the output connects to the input is about 1% less than the output's open-circuit voltage. If the input side has a smaller impedance (10kΩ is frequently seen with "passive" modules), or the output side is higher, then the apparent "loss" of voltage may be much greater.
However, that is partly Eurorack's own fault for treating the output open circuit voltage as the normal expectation and anything less as "droop." In other subfields of electronics, it is usually expected that inputs and outputs will have similar, ideally equal, impedance, and the voltage that results from matched impedances is treated as the normal expectation. Having equal input and output impedance maximizes (for a fixed output impedance and open-circuit voltage) the amount of power delivered to a load, which is important in a situation like an amplifier driving a speaker where power is expensive and you want to conserve it. You can prove that for yourself with a little bit of first-year calculus: fix V1=1, V2=0, R1=1, write an expression for the power (voltage times current) in R2 as a function of R2, and maximize power.
With matched impedance, the output voltage under load is theoretically half what the output voltage would be into an open circuit; but "open circuit" may not even be a normal operating state in which you could get a valid voltage measurement. Some radio amplifiers are actually damaged by operation with open-circuited outputs.
When a radio transmitter drives an antenna through a cable, the cable itself has a characteristic impedance, too. You want your transmitter to match the cable at one end, and the cable to match the antenna at the other end; mismatches cause the signal to be reflected back in the opposite direction, which causes a variety of problems. In high-speed digital work, this kind of thing can even happen at the scale of traces on a circuit board: the chip sending a signal needs an impedance match to the circuit board trace which then also needs to match the chip receiving the signal, else there will be reflection. Reflection from impedance mismatches is seldom an issue at audio frequencies.
Thinking in terms of equivalent circuits helps with understanding why it's undesirable to patch outputs to outputs. If R1 and R2 are both zero and V1 and V2 are not equal, what happens? In principle, an infinte amount of current flows! That cannot really happen because the outputs cannot supply so much current; what will really happen is that the assumptions behind the equivalent circuits will break. For instance, if an op amp has an in-the-loop current-limiting resistor, it will have zero output impedance only as long as it doesn't clip. Connecting two such circuits together, when they disagree on the output voltage, will create a situation where V1 and V2 are at or near opposite power rails (because the op amps clip) and then R1 and R2 are the output resistor values. From there we can easily calculate the current, which will be large but not actually infinite.
If you are designing in a context other than Eurorack and want to make it so that you can mix outputs just by patching them together, then you might deliberately give your outputs higher impedance - but then there will be a larger gap between the output open-circuit voltage and the voltage actually realized when you patch into an input. Unless, of course, you try to make the input impedance infinite or effectively infinite, which has its own problems. Careful attention to equivalent circuits makes it possible to understand how these trade-offs will play out.
Impedance is useful for understanding what's going on with electric guitars, too. Someone recently asked me, "Can I plug my guitar directly into my Eurorack?" Well, assuming you have a 6.35mm to 3.5mm adapter, that is physically possible; but it won't work very well because an electric guitar has a very high output impedance, usually tens to hundreds of kΩ. If you plug it into an oscilloscope, which might often have 1MΩ or 10MΩ input impedance, the guitar may appear to produce a fair bit of output; but plugged into a typical Eurorack input with an input impedance of 100kΩ (still very high by general electronic-equipment standards, but much less than the scope) you won't actually hear much signal. Setting R1=500kΩ, R2=100kΩ, V2=0 in the circuit above demonstrates the problem: voltage through R2 is only one sixth of the voltage at V1, with most of the signal disappearing inside R1. Preamps, pedals, and amplifiers designed to take input directly from a guitar will often have input impedance in excess of 1MΩ, to eke out as much signal as possible at the input before they start amplifying it.
Norton equivalent circuits
There is a lot of mathematical duality in electronics. If you have a true statement about circuits, and you swap the concepts of voltage and current, series and parallel, and inductance and capacitance, quite often you get another true statement. This kind of symmetry is related to the symmetries that come up in modern physics, where they are studied using group theory.
Duality applies to equivalent circuits. The Thévenin equivalent circuit discussed above has a given open-circuit voltage and a given short-circuit current, and it linearly interpolates between those two points. Any other circuit which had the same open-circuit voltage and short-circuit current and linearly interpolated between them, would also serve as an equivalent circuit.
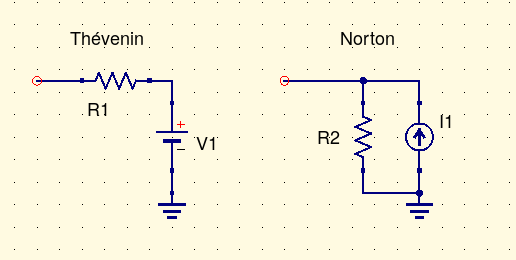
For example, we can change the series resistor to a parallel resistor and the constant voltage source to a constant current source, and get a new equivalent circuit that also works, which is called the Norton equivalent circuit - from Norton's Theorem, independently derived by Edward Lawry Norton of Bell Labs and by Hans Ferdinand Mayer of Siemens, both in 1926.
The symbol labelled "I1" may be unfamiliar: that's a constant-current source. The current through it is always equal to some constant value. With nothing else attached (open circuit) the current through I1 must pass entirely through R2, developing the open-circuit voltage. With a short circuit attached, R2 is out of the picture and the current from I1 entirely flows through the external short circuit. From those facts we can calculate that the resistance (equal to the input or output impedance) is the same between the two circuits: R1=R2. And the voltage and current sources are related by Ohm's Law through that resistance: V1=I1·R1, I1=V1/R1.
The Norton equivalent circuit is probably less often used than the Thévenin equivalent circuit because people tend to think of voltages as the main event when describing signals - especially in the Eurorack world where input impedance tends to be high and uncontrolled and current tends to be seen as negligible. But the Norton equivalent circuit is worth knowing about, and it sees some use in contexts where current is the main focus of attention. Calculating the result of putting two Norton equivalent circuits in parallel is a little easier than doing the same with Thévenin circuits because the current source values simply add, instead of requiring a voltage-divider calculation; there is a parallel-resistance calculation in either case.
There's a special kind of op amp, exemplified by the LM3900, which holds its inputs near the negative rail and has its output go high or low according to the difference in current flowing into the inputs, instead of the difference in voltage. This is called a Norton op amp with the name "Norton" basically just interpreted as meaning "using current instead of voltage." This chip is used occasionally in synth circuits - in particular, it occurs in the Serge SSG circuit. With so many other things, like OTAs and exponential converters, having current output, it's sometimes convenient to have a thing like an op amp but with current input.
More complicated equivalent circuits
When designing circuits we constantly face the gap between theoretically ideal concepts like resistance, capacitance, and inductance; and the real-world behaviour of components like resistors, capacitors, and inductors. A resistance is anything that passes a current exactly proportional to voltage, obeying Ohm's Law; a resistor, on the other hand, is a physical object built for that purpose, which may or may not really do it well. Real-world resistors may do things like develop a magnetic field (especially if they happen to be wire-wound resistors) so that the current increases a little bit over time at a constant voltage, which is not what Ohm's Law says should happen.
Similarly, the current through a capacitance should be proportional to the first derivative of the voltage, whereas the current through a capacitor is usually well-approximated by that, but also subject to other effects; and there is often a significant gap between the idealized and real-life behaviour of inductances and inductors.
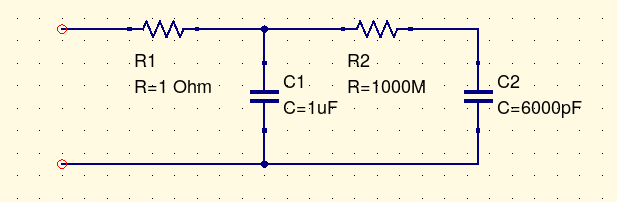
When talking about the non-ideal behaviour of components, it's often useful to draw an equivalent circuit that describes what the component really does, in terms of idealized circuit symbols. Once we understand the behaviour of the idealized concepts we can use them as a language for describing non-ideal effects. For example, some capacitors exhibit an effect called dielectric absorption or "soakage." You charge one up, discharge it with a short circuit, remove the short and wait, then measure the voltage across the terminals, and find that it's not zero. What happened - where did that charge come from after you removed it all?
Well, we can talk about the physical effects involved, which come down to molecules being rearranged in the dielectric to form a semi-permanent "electret" analogous to a permanent magnet. But we can also draw an equivalent circuit. The capacitor functions as if it had a little bit of extra capacitance in it, hidden behind a large resistance.
From the as-if circuit we can make correct guesses about what the capacitor will do. The R2/C2 section has a time constant of 0.17 seconds. If you charge the capacitor with a constant voltage for a few seconds, both C1 and C2 will charge up. If you short it briefly, you get a spark as C1 discharges through the stray resistance R1, time constant 1µs. (The resistance 1Ω may actually be a little high, but that was convenient to put in the screenshot.) But if you discharge it for less than a second or so, C2 won't have time to discharge fully. Leaving the capacitor open for several seconds allows the remaining charge in C2 to drain into C1, and then when you measure it again, you find a small charge on C1 again.
Nobody is claiming that your single capacitor is really two capacitors; but the equivalent circuit is realistic in a different way, because it represents what the capacitor really does in a way that a pure abstract capacitance wouldn't.
Equivalent circuits used to describe component behaviour may be simple or complicated as necessary to represent whatever effects they are meant to cover. As well as describing non-ideal behaviour of passive components like capacitors, they can be useful in explaining how active components like transistors work. For example, here is a Qucs version of the "hybrid pi" model for a bipolar transistor. All the components shown correspond to measurable physical effects in a real transistor; within the scope covered by the hybrid pi model, the real transistor behaves as if it contained this circuit.
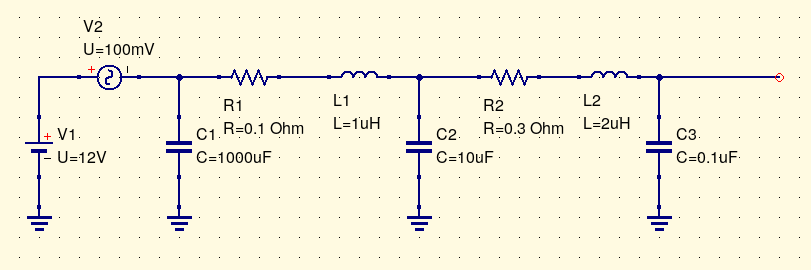
Equivalent circuits need not be limited to just modelling individual components. Here's an example of how an equivalent circuit might be used to describe what's going on in a power distribution system.
The power supply functions like a 12V DC voltage source, but it doesn't produce pure DC; I have also included a 100mV AC source representing ripple or noise (which might even be two separate sources in a more elaborate model). The supply has a built-in filtering capacitor, but all that is separated from the rest of the system by some wiring, which has both resistance and inductance (shown by R1 and L1). Then the wire arrives at a circuit board, which has a smaller 10µF filter capacitor of its own. From there, to get to a chip the power has to pass through traces on the circuit board, with resistance and inductance shown by R2 and L2; then the chip has its own local bypassing capacitor of 0.1µF. Depending on the level of detail and the frequencies we were interested in, we might even include additional equivalent components for stuff like the inductance of the bonding wires inside an IC package. All the numbers shown in this image are made-up to be illustrative, but not to accurately represent any particular real system. An equivalent circuit model like this one could be useful in estimating how much impact different design decisions would have on the levels of noise and ripple in different parts of the power system.
To conclude: I've described the general idea of equivalent circuits as "as if" circuits, simplified or idealized circuits that express the behaviour of other circuits within a limited scope. I've gone into some detail on the Thévenin equivalent circuit, consisting of a voltage and a resistance, and discussed the concept of input and output impedance, which is equal to the resistance (or more general impedance in case of AC) in the Thévenin equivalent circuit. I've also touched on the Norton equivalent circuit consisting of a current source and resistance, and the more complicated equivalent circuits sometimes used to model non-ideal behaviour of real-world components. It's important to be able to think about equivalent circuits as a basic competence in designing and understanding electronics.
◀ PREV Do you really want that scope? || Module wear and aging NEXT ▶