Modular synthesis intro, part 10: Analog oscillators
2018-04-01 intro
This is Part 10 of a series that started with Part 1.
Once you have an electrical signal that represents a sound, you can process it into music with such modules as filters and VCAs. But where does that sound come from in the first place? Quite often, the audio signal originates with an oscillator - an electronic circuit that produces a repeating waveform - and for anything but the most static kind of drone music, it's usually a voltage-controlled oscillator, or VCO, which changes its pitch under control of a voltage from other modules. In my metaphor of a subtractive synthesis patch being like a saxophone, the VCO is like the reed. Waves from it are then shaped by the body (which is like the filter); turned on and off by the player's mouth and lungs (like a VCA), and have their pitch controlled by the keys (which are like control voltage generators). A similar mapping exists between modules and the parts of other acoustic instruments.
Just as a saxophone reed won't sound very good if you detach it from the rest of the instrument and try to blow on it alone, the raw waveforms from the oscillator may not sound good all by themselves. That becomes less true in some of the "West Coast" patches where there's a lot of modulation applied directly at the oscillator instead of through filtering. But even there, it's common to process the oscillator waveform instead of using it directly. As a result, trying to chase the perfect sound by picking a special oscillator may not be the best way to choose modules; nonetheless, people do it.
In this installment I'm going to talk about the most common kinds of analog oscillator circuits - how they work in very general terms and what you need to know to start using them. My plan is to cover digital oscillators two weeks from now in Part 11.
Voltage control
As I think I've mentioned before, human senses tend to operate logarithmically. That is to some extent necessary in order for our senses to be able to cover wide ranges of physical phenomena while still being useful at both ends. It is especially true in the case of our perception of sound frequency, where the logarithmic relation is quite exact. If you listen to a 220 Hz tone followed by a 330 Hz tone, the difference between them sounds like a certain amount, which happens to be called a "fifth" for ridiculous reasons; but then the difference between the 330 Hz tone and an 495 Hz tone, even though it is 1.5 times as many Hz, sounds like the same amount of difference - one fifth. Our ears hear frequency ratios, not absolute frequency differences. Here's a sample of those tones (software-generated sawtooth waves), first the 220/330 and then the 330/495 pair:
Both to make it easier to connect voltages with perceived pitch, and for the same dynamic-range reasons that it's useful for our ears to work logarithmically in the first place, the control voltages for VCOs usually also work in a logarithmic fashion - a given change in control voltage results in a given change in proportion of the output frequency. For Eurorack, the standard is 1V/octave, meaning that for each additional volt of control signal, the output frequency doubles. If the tuning knobs are adjusted so that the oscillator runs at 220 Hz (A below middle C, in standard concert pitch) at 0V of control input, then increasing the input voltage to 1V will produce an output one octave higher (440 Hz, A above middle C). Control voltage is a logarithmic function of output frequency, and conversely, output frequency is an exponential function of control voltage. Whether you want to call that "logarithmic" or "exponential" control depends on your point of view.
Other control voltage standards are possible. Some non-Eurorack modular formats use instead a 1.2V per octave system; that way, it's easy to read off the number of semitones with a voltmeter (each octave is 12 semitones, each semitone is 0.1V). There are also systems which do not use the logarithmic voltage/frequency relation, but instead a linear one usually called "Hz/volt"; then to double the frequency you must actually double the voltage. For Eurorack, though, it's usually assumed that a VCO will have at least one 1V/octave control input.
A question can arise, especially with analog circuitry, of how accurate the 1V/octave control really is. When you raise the input voltage by 1.000V, is the frequency really multiplied by 2.000, or is it more like a factor of 1.948, or 2.033? Because human ears can detect certain frequency ratios to very high accuracy, it's important that oscillators "track" their 1V/octave inputs well. Poorly-tracking oscillators will play out-of-tune music, and even if you want some sloppiness in your tuning to make it sound "more analog" (whatever that means), the old saw applies: you can always de-tune your oscillators, but you can't add precision that was never there to begin with. So it's important that VCOs used for main musical content should be built to good standards of precision.
Compounding the problem, virtually all analog VCO circuits with V/oct input depend on the exponential voltage-current characteristic of bipolar transistors... and that behaviour is highly temperature sensitive. An oscillator that tracks perfectly for one moment may go sharp or flat within minutes as it is warmed or cooled by an imperceptible breeze. Designers put a lot of effort into preventing or compensating for the effects of temperature changes. Digital oscillators, although still subject to this issue to a measurable extent, often end up more temperature-stable than analog oscillators and are usually thought of as perfectly stable.
Features and extras
The simplest possible VCO might have a V/oct input, an output that plays some fixed wave shape, and a tuning knob, which controls what frequency comes out at 0V of control voltage input. There is normally no fixed value for the frequency at 0V. I'll say that again, because it's a commonly-asked question and a common misconception even among people who should know better: there is normally no fixed value for the frequency at 0V. It's just whatever frequency you set with the tuning knob, modified by a ratio controlled by the control voltage. This is important, for instance, when you use a VCO with no control voltage, just turning the knob, to generate "drones"; also important for connecting to different MIDI interfaces, which do have standards for what 0V means and may not agree with each other.
Oscillators may differ in the details of their manual frequency controls - just one big knob for frequency, separate coarse and fine knobs; high and low ranges selected by a switch; switches specifically for going up and down an octave at a time (one of North Coast's modules can add this feature to oscillators that don't already have it); and so on.
Beyond having a V/oct input and a tuning knob, most VCOs have at least a few additional features. Quite often, there are two or more outputs offering different waveforms. Since these waveforms are all derived from the same oscillator core by different processing of a single native waveform, the outputs will all be necessarily synchronized at the same frequency. Maybe, at a stretch, they could be in simple ratios - having a "sub" output at half the core frequency is a fairly common variation, for instance. But you're not going to see two outputs at separately controllable frequencies except in a multi-oscillator module that actually contains separate cores for the different frequencies.
Modulation inputs are often seen. Exponential FM (frequency modulation) is another input that affects the pitch by a voltage-controlled ratio multiplied in with the V/oct main pitch control. There'll usually be an attenuator knob for controlling the sensitivity of the exponential FM input; roughly 1V/octave (same as the main pitch input) is a typical maximum, but that is often more than people really want to use, so they will dial down the sensitivity to achieve the desired effect. There can also be linear FM inputs, which change the frequency as a linear function of the input.
With V/oct and exponential FM, any positive or negative input voltage always corresponds a physically meaningful frequency greater than zero. But with a sufficiently strong signal on a linear FM input, it's possible to command the oscillator to produce an output frequency less than zero, and it's an interesting question what happens then. Basic, traditional analog oscillator designs will just stall at zero frequency, with their output assuming a fixed non-oscillating DC voltage until the commanded frequency becomes positive again. But it's also possible to build an oscillator core (usually with considerably more circuitry and expense) that will run backwards in such a case, with its output waveform reversed in time. Oscillators designed to do this usually call it a "through-zero FM" (TZFM) feature, and it can be a musically interesting effect. I may discuss it more in some future article. For now, just be aware that it exists, and if an oscillator supports it, the manufacturer will usually make that very clear because it's considered a big selling point.
Many oscillators offer a way to change the shape of the waves under voltage control. The simplest case is probably pulse-width modulation (PWM). A pulse wave just switches between two voltages at a given frequency, and there's a distinction possible as to how long it stays at one or the other. It is high and low for equal amounts of time? Is it just a short blip of "high" and then "low" almost all the time? The harmonic content changes depending on this ratio, and it's often possible to adjust the pulse width with both a front-panel control and a control voltage. Some analog oscillators also offer other kinds of shape-changing features, although probably none come close to the extra wave shape modulation achieved by digital wavetable oscillators.
Modulation is one way to combine two oscillators to produce a single audio spectrum, but another popular one for analog oscillators is by synchronization or sync. In "hard" sync, the most traditional kind, two oscillators called master and slave are linked so that every time the master oscillator starts a new cycle, the slave also returns to the start of its own cycle, even if it was in the middle of a cycle. The slave would usually be set to a higher frequency, so it may complete several cycles of its own before each time the master resets it. (The explanation of sawtooth cores in the next section may make this process a little clearer). The result is that the slave's output has a spectrum emphasizing frequencies near those it would produce on its own, but also restricted, because of the ongoing resets, to multiples of the master's fundamental. Some oscillators support a "soft" sync mode instead of or in addition to "hard" sync; exactly what that means depends on the design, but it usually involves sometimes but not always resetting the slave when the master cycles, subject to some sort of conditions. Soft sync typically produces a similar but less extreme kind of sound compared to hard sync.
Sawtooth cores
This is a device you sometimes see in traditional Japanese gardens:

It's officially called a shishi-odoshi (鹿威し), but to English speakers it's often "the thing that goes klunk."
In this device, there's a steady, continuous flow of water (upper right in the photo) which pours into a bamboo tube on a pivot. The tube has an obstruction near the centre, so the water fills it up only on the high side, which becomes heavier and heavier. Eventually, the high side full of water weighs more than the empty low side, and so the tube tilts on its pivot. The water falls out, the low side is the heavier side again, so it tilts back up, and the end of the tube smacks against the rock. "Klunk!" Then the mouth of the tube is in the path of the water again, so it starts filling up once more. With a steady, unvarying stream of water, the thing goes "klunk" at a steady, unvarying rate, typically once every few seconds. It is supposed to frighten away animals such as deer, and create a contemplative mood in the garden.
If the water were flowing faster, the tube would fill up sooner and the thing would go "klunk" faster. With less water, it would go "klunk" more slowly. Under ideal circumstances (with no water lost over the edge or wasted during the reset process) we could imagine that the rate of klunking would be directly proportional to the flow of water - making this a water-controlled klunker (WCK). Analog VCOs often work on a similar principle.
In the core of a traditional sawtooth-core analog synth VCO, there is usually a single capacitor that charges continuously from a circuit (called the "exponential converter") that offers a steady trickle of current. The voltage across the capacitor increases as it charges. When the voltage exceeds a preset threshold, it triggers a reset circuit which quickly drains all the charge out of the capacitor, after which it starts charging again. All this is very much like the bamboo tube that fills with water and then dumps out. And just as in the water-controlled klunker, the capacitor in the voltage-controlled oscillator can be controlled by changing the flow into it. The V/oct voltage, the tuning knob or knobs, and any frequency modulation inputs all feed into the circuit that provides charging current to the capacitor. How fast it charges, and therefore how often it is emptied, is proportional to that current, and it can be varied over a wide range usually with a fair bit of accuracy in the proportion.
The voltage across the capacitor, buffered by an amplifier to prevent outside loads from interfering with it, is the main output of the oscillator. It looks something like this:
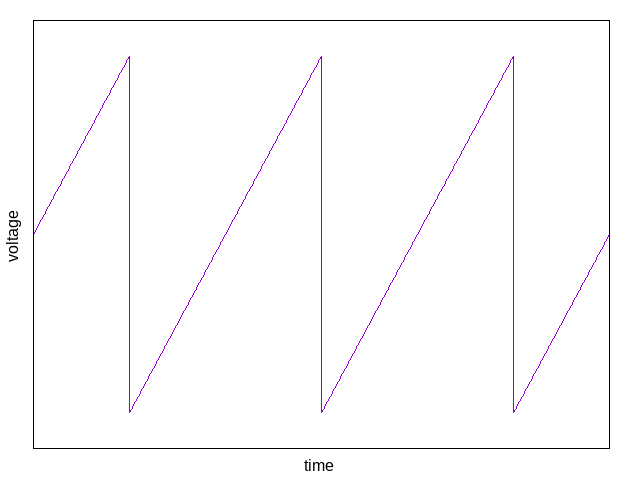
That's a very useful waveform because it is rich in all harmonics of the fundamental frequency. It sounds rather harsh by itself, but it is a fine input for filters that produce a wide range of timbres. Because they are both useful and easy to generate, sawtooth waves are probably the most traditional oscillator waveform in "East Coast" subtractive synthesis patches. And modular-synth VCOs often use this "sawtooth core" design. To offer other waveforms, they may process the core's sawtooth in various ways to generate other shapes. For instance, by setting a cutoff voltage somewhere between the top and bottom and using a Schmitt trigger (see my earlier article about that) to generate a high voltage when above the cuttoff, low when below, the result is a pulse waveform; and pulse-width modulation comes about by changing that cutoff voltage.
Triangle cores
Another popular style of analog synth VCO also uses a capacitor that charges and discharges according to a control current, but without a sudden "reset" operation. Instead, there is a switching circuit that applies the same current in opposite directions to both charge and discharge the capacitor at a voltage-controlled rate. In some cases, doing it this way helps achieve more precise V/oct frequency tracking. The resulting core output voltage looks like this:
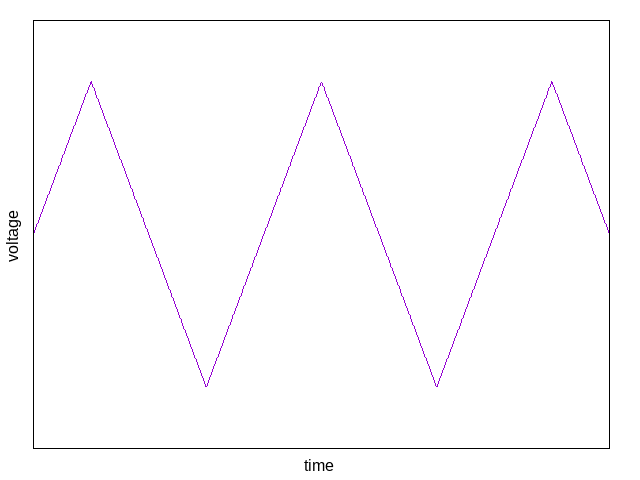
I used this kind of core in my own design of the Middle Path VCO. The triangle waveform is much less rich in harmonics than a sawtooth; it is relatively close to a pure sine wave. That can make it more musically desirable by itself; but it may also require processing to change the waveform before it will be good fodder for subtractive filtering. As with the sawtooth core, triangle-core oscillators often include some processing circuits to generate other waveforms from the core output. Because of the different switching arrangements inside the core, the reset and through-zero features that are easy to design into a triangle-core oscillator may be different.
Oscillating filters (sine cores)
Instead of charging a capacitor linearly and switching sharply between different states, it's possible to construct a circuit that processes signals at different frequencies in a smooth, continuous way without any sharp switching, and happens to do it in such a way that the output will naturally settle into a repeating pattern. These kinds of circuits are usually best understood as filters with feedback, and in fact, if you literally take a synthesizer filter and feed its output back into its input, there's a good chance that it will create a sine waveform.
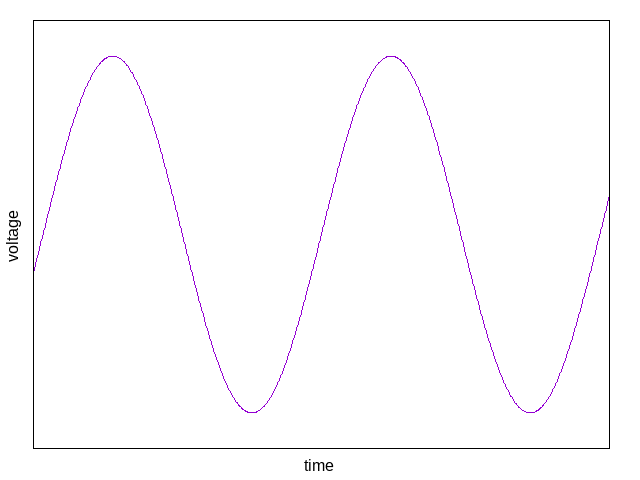
One can design a filter-like circuit specifically meant to be used for generating sine waves, and then it might reasonably be called a "sine-core oscillator" (though that term is not especially common).
Pure sine waves have no harmonic content beyond the fundamental at all. If you have many of them at different frequencies, you can do additive synthesis; and they may be musically desirable for drones and as modulation sources. To use them as input to filters, though, you will probably want to apply some kind of distortion to create additional harmonics, even if it is as simple as overdriving the filter input with a very strong sine wave.
Modules sold primarily as filters can often be pressed into service as sine-core oscillators, but be aware that it may be difficult to get them to track accurately. Some filters have no V/oct input at all, and even for those that do, it may not be temperature-compensated. The North Coast MSK 007 Leapfrog VCF is one of the few Eurorack filters with an accurate temperature-compensated V/oct input. I'm a big fan of sine cores, and I also put eight of them in the Fixed Sine Bank - which is not a VCO because the oscillators are not voltage-controlled nor controllable at all, but it's a (multiple) sine-core oscillator.
"Complex" oscillators
The term "complex oscillator" is usually associated with Buchla and the West Coast tradition. Modules sold under this name usually consist of two or more analog VCOs with designs similar to those described above, with built-in features to help when using them to modulate each other. For example, there may be switches and an internal "bus" for applying one oscillator's output to modulate the other without needing to run patch cables between them. Often the "complex" oscillator will also contain some processing functions, such as a wavefolder unit, that can be optionally applied to the outputs of the oscillators. All these effects could also be achieved by patching together conventional non-"complex" VCOs and other modules, but it can be nice, and artistically valuable, to have them conveniently combined in a single package.
The North Coast Synthesis Ltd. MSK 013 Middle Path VCO is a good example complex VCO. It includes two analog oscillator cores (triangle-based, as discussed above), a sync circuit, and a modulation section that can create sine waves, phase modulation, and wavefolding effects using the outputs of the built-in cores or external inputs.
Low-frequency oscillators (LFOs)
If an oscillator runs at an especially low frequency (in particular, below the lower limit of human hearing at 20 Hz), it can be called a low-frequency oscillator, or LFO. It's often useful to have an oscillator running at a low frequency to modulate others; and some modules (including my own Fixed Sine Bank) are designed for that role. They may or may not be voltage-controlled. Many dedicated LFO modules only have knobs for the frequency with no voltage input. Manual control, or no control, can make the modules much cheaper and simpler than an accurately-tracking V/oct VCO would be. Even a voltage-controlled module intended for LFO duty may not be designed to track accurately, in the way that would be expected of a VCO used for main musical content. In the other direction, a standard VCO can often be driven to low enough frequencies for LFO use, even if it is a relatively expensive way to get that capability, and some VCO modules are sold under the name "VCO/LFO" to make clear that they also work well at low frequencies. The point here is that there is no hard distinction between what is an LFO and what is a VCO; those terms tend to be applied more according to how the module is being used in a given patch.
I've described some of the main kinds of analog synth VCOs you are likely to encounter in the modular world. There are many smaller and more specialized variations; and in a subsequent article I plan to discuss digital oscillators, which in many cases offer very different musical effects.
Continue to Part 11 of this series.
◀ PREV News, reviews, and demos || Transistor Mixer press release NEXT ▶

