Walking the hypercube

2018-06-20 math composition music

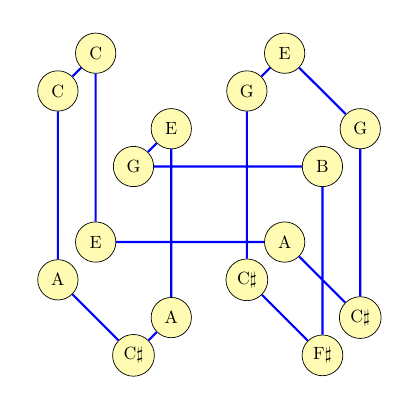
Here is the skeleton of a four-dimensional hypercube, or tesseract, with the vertices labelled by musical note names.

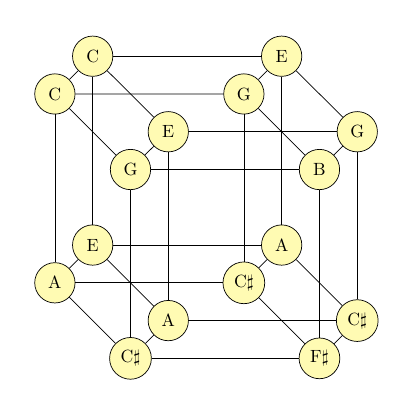
No label is used more than three times, and out of the 24 two-dimensional faces of the tesseract, on 18 of them the note names form a major or minor triad with one note doubled, or a seventh chord (major triad plus minor seventh).  The number 18 is the maximum possible given the other constraints, in particular the "at most three uses of each label" limitation.  So... what's the point of this?

I'm interested in finding ways to automatically generate music that will have some of the structure and beauty of human-written music.  In this day and age, we ought to be able to do better than the "noise into sample and hold" patch for generating random melodies; how can we do something more musically informed, but still randomized and automated?

One idea I've used before is to have agents moving around some kind of landscape with their motion translated into musical notes; you may recall my Notes on notes on the plane.  That was based on tilings and associating notes with directions of movement.

With the tesseract I'm doing something a little different:  throwing out Euclidean geometry in favour of graph theory, meaning that directions, and locations in space, no longer have meaning, only the vertices and the edges between them, and then connecting vertices instead of directions with the different notes.  If an agent starts on one vertex and then moves in some pattern, playing each note encountered, how does it sound?

I'd like the music to sound like music, meaning it has some kind of harmony or key and some recognizable pattern.  That's one reason for choosing the vertex labels to form chords.  If my agent is spinning around one of the faces of the tesseract, it'll be (three quarters of the time, 18 faces out of 24) arpeggiating a chord.  If it takes a more complicated path it will produce more complicated output, but my hope is that the structure of the graph will still guide it into somewhat musical patterns, both vertically (harmony) and horizontally (melody).  Here's a first attempt.

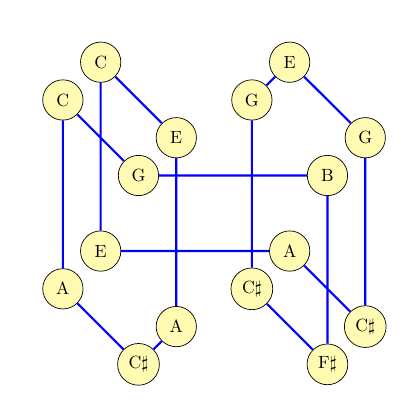
I've chosen just a subset of the edges of the tesseract so that they form a cycle covering the 16 vertices.  With a selection of octave applied to each vertex, running around the cycle gives a looping 16-note sequence.

As you can hear from the audio, it doesn't sound wonderfully musical, but it at least has a recognizable key and a bit of recognizable structure.  I think it's at least better than just purely random noise through a quantizer, and it's comparable to the stuff that people use as seed sequences or starting points in improvised modular-synth music.

One thing that would help would be  if the sequence could change over time in some kind of musically coherent fashion.  I'm thinking of the kind of thing we do with the classic Turing Machine module (hate the name because I want to use literal Turing machines for musical purposes and now if I try, everyone will misunderstand what I'm doing; but that's another rant).  I'd like to have some way of changing the sequence randomly, a little at a time, so that each new version is somehow close to the old one, and they all sound musical at each step along the way, but the changes can accumulate and eventually it's completely different.

Suppose I'm playing through a cycle in the tesseract, as above, and then I choose one of the four-edge faces of the object, such that it happens my current cycle contains exactly two opposing edges of the face.

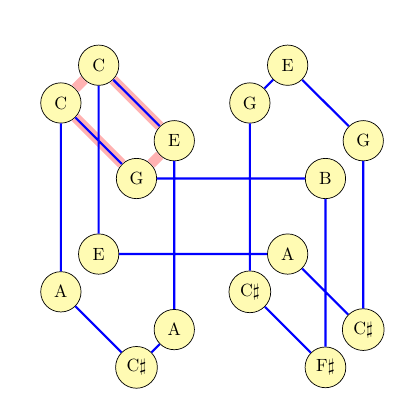
I can flip that face - remove the two cycle edges it contains, and add in the other two - and I'll still have a cycle cover of the tesseract.  That means a set of one or more cycles covering all vertices.  In the example above, flipping the edges gives another single cycle covering all 16 vertices (a Hamiltonian cycle, in math terminology):

Playing through that cycle gives a new and different 16-note sequence.

It still sounds a lot like the previous sequence, but it's also not exactly the same.  Doing the graph flip has had the effect of rearranging the notes, but not completely.

Doing a graph flip does not necessarily keep the "cycle" in one piece; it could be that a flip would separate the chosen edges into a set of two or more cycles not connected to each other.  We could end up with the agent that moves around the tesseract stuck in a loop of less than 16 notes, or if there are multiple agents, they could be in separate loops, even of different lengths.  That's why I call it a cycle cover, not necessarily a cycle; it is always at least a set of cycles covering the vertices, if not a single cycle.  Cycle covers, especially of hypercubes, were something I spent a lot of time on a few years ago when I was doing math research.  But having a more general cycle cover instead of necessarily a single cycle covering all vertices may be a feature, not a bug - more musical possibilities when the loop of notes can change lengths.  The properties of the tesseract graph (in particular, the fact that it is bipartite) at least guarantee that the cycles will be of even length - maybe 4, 6, or 8 notes, but never 3 or 5.  I think that helps keep it to a musical rhythm.  The profusion of length-4 cycles (faces) in the tesseract also creates many opportunities for doing these edge flips.

So that provides an outline for generating evolving sequences:  label a tesseract with musical notes (I think it's a good idea to do this in a way that maximizes chords, but other ways are worth exploring, too); maintain at all times a cycle cover which provides paths among the vertices; have agents moving around the cycle cover playing notes as they encounter vertices; and change the cycle cover every so often, like a Turing Machine module changes its sequence, by way of face-edge flips.

I programmed up a control voltage generator following that outline (with some added rules for dealing with collisions between agents, and so on), loaded it into my homemade "computer in the rack" Eurorack module, and let it run for a while.  Here's the result.

There are four agents exploring the graph in that track, in a doubling sequence of speeds:  one generates eighth notes, one generates quarter notes, one half notes, and one whole notes.  I started out with the cycle cover set to four disjoint faces of the tesseract, with each agent on a different face repeating a four-note cycle and never colliding with the other agents.  You can hear the very repetitive sequence at the start of the track.  Then as "flips" happen, the cycles join and mutate, the agents start to interact (I'm not allowing them to collide, so each one reverses direction if it would attempt to move into another agent's vertex, or stays where it is if crowded in on both sides), and the music gets more complicated.  Patching four separate voices on my little three-row synth required stretching some of the hardware to the max; I am using two traditional synth oscillators but also a Hikari Sine and one of my own North Coast Leapfrogs patched as a sine-wave VCO, in order to get four independent V/oct notes at once.  Only the two faster voices have amplitude envelopes, demoing the soon-to-be-released North Coast Transistor ADSR modules.  I'm also using North Coast modules for octave switching and mixing with distortion.

All in all, although this technique clearly doesn't just generate good music straight out of the box without manual wiggling, I think it's at least as good as the kind of mutating sequences that come out of a Turing Machine module, and people clearly get a lot of compositional inspiration out of that.  The software I used is in no shape to be shared (one-off ECLiPSe-CLP command lines, C customized to my homemade module, etc.) but if there's significant interest I could share some more details on the techniques used.  I don't expect to build a "Tesseract Machine" module that would implement this exact algorithm as a hardware device people could slot into their racks, simply because I don't think it would sell.  I have a hard enough time getting sales on much less specialized modules.  But it's certainly going into the hopper of ideas that might possibly find their way into future North Coast modules if North Coast can stay in the business of developing new modules.

There are a number of interesting math and musical questions one could delve into.  Is it always possible to find at least one flip in any cycle cover?  I think so, but haven't proved it.  Supposing we can do that, can we always get from one cycle cover to any other by some sequence of flips?  My guess is that's also a yes, but I'm less confident of it.  My gut feeling was that making the vertex-labelling rich in chords (by maximizing the number of faces where the notes on the face form a chord) was likely to generate music that would sound good, but I haven't tried very many other possibilities.  The labelling I used in this track used the constraint of no more than three copies of any note, but I've also done searches and found chord-maximizing labellings for each possible value of "three."  With no duplication of notes allowed (and the standard 12 note names) no labelling is possible because there are 16 vertices; with at most two copies of any note, it's possible to get 16 chords; with three, 18 (as above); with four, 22; and with five copies of some notes, it's possible to have all 24 of the tesseract's faces form chords.  That's allowing major, minor, and seventh chords; of course one might also allow a different set.  Changing the labelling could be expected to make the music sound different.  And, although I wanted a graph with very many four-vertex cycles, it's easy to imagine using other graphs instead of the tesseract in particular.

◀ PREV State of the store || Tools for getting started with SDIY NEXT ▶