tag "math"
AoC 2024 in ECLiPSe-CLP
This year a friend challenged me to do the Advent of Code challenge (AoC) in Prolog. This is a sort of test of software engineering skills: the organizers of the project post a series of puzzles, two per day from December 1 to December 25. It's not the kind of thing I usually do and not the kind of thing I usually post here; but I thought it would be fun to try once, and having put in the work, I'd like to get as much value from it as possible - so I'm posting my solutions and some notes about them here. If you're coming to this page from a software engineering source, I hope you'll stick around and take a look at my products before leaving the site. READ MORE
Remote-debugging the Gracious Host
The MSK 014 Gracious Host is meant to work with all standards-compliant USB MIDI devices, but that's often easier said than done. I had some adventures recently when I helped a customer get the Gracious Host running with a Teenage Engineering OP-1 (original, not "Field"), and it makes for a good story. READ MORE
Outrunning the Noise Bear
Somewhere in the far North, in fact on the North Coast, the Tenderfoot module was new in town, and a grizzled old A-110-1 was showing him around. As they passed the Rack Brute Saloon, the old timer warned the newcomer about the Noise Bear. READ MORE
Smith chart by projection
I want to use a Smith chart in an upcoming article here, but it occurs to me that most readers probably aren't familiar with them. Smith charts don't come up very often in audio, being mostly an RF thing. So as with complex numbers, I'm posting this separate article to introduce Smith charts, and then I can refer back to it when I use them later. READ MORE
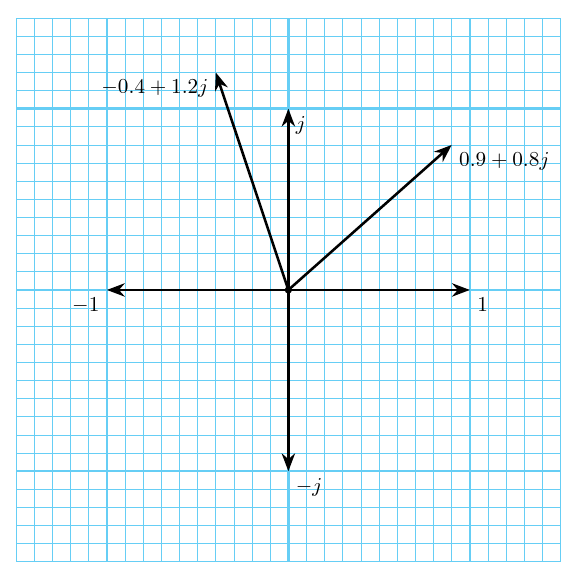
Why you need complex numbers
I plan to use complex numbers in an upcoming article, and I thought I'd better post some introductory material about them first. Of course, there are many introductions to complex numbers on the Net already and there may not be much new I can say; so rather than focusing on what complex numbers are, which you can find almost anywhere, I thought I'd come in from a different direction and talk about why you should care about them. READ MORE
A fractal sequencer toy
Here's a fractal chord sequencer you can play right in your browser. READ MORE
Aconcagua
Every so often I come back to the idea of generating self-similar or "fractal" chord progressions by recursively applying grammar rules, as in my 2015 composition Dharmapala. I like the general method described in that article, but one thing I don't like so much about the finished piece is that it sounds the same all the way through. There's a little bit of "development" or shift in texture over the course of the piece, largely driven just by my performance-time changes to the synthesizer settings and the fact that I allow the notes to be chosen from a wider range toward the end. READ MORE
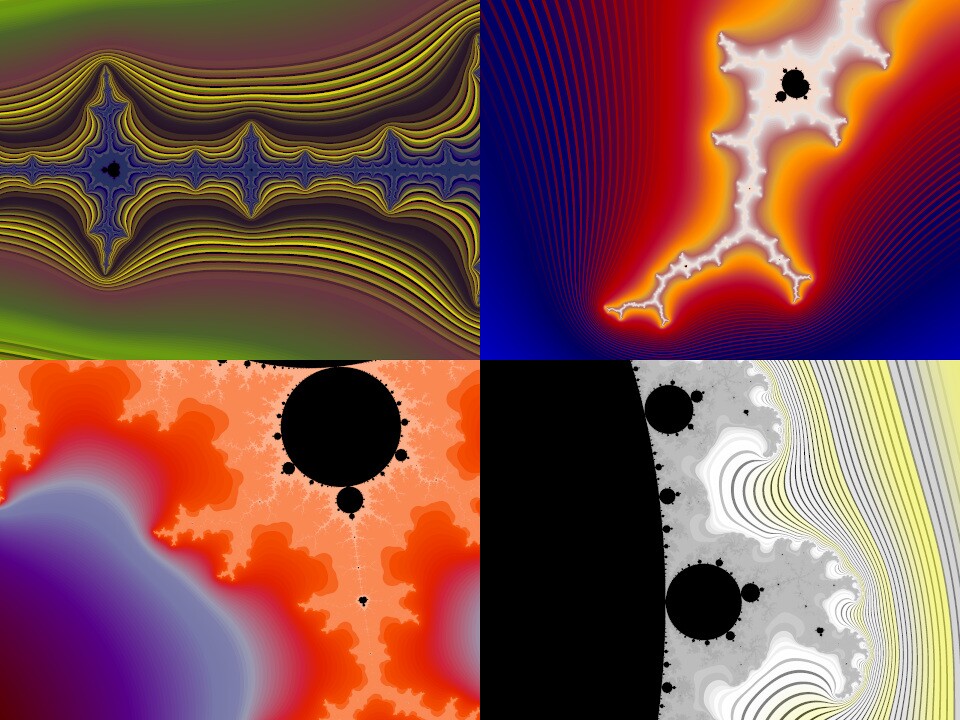
Listening longer to the Mandelbrot Set
I've long been interested in ways to sonify fractals, and I wrote an article here about Listening to the Mandelbrot Set in 2017. At that time, I was thinking of it as a way to generate a waveform: basically, imagine running a point along the (infinitely wiggly!) boundary of the set, making many complete circuits per second, and use the real and imaginary coordinates of the moving point as waveforms for synthesis. Then the entire Mandelbrot Set (often abbreviated to "M") defines a timbre that may be interesting, and which can be used as a musical building block. It's a little bit like putting a phongraph needle on the edge of the set and playing it like a record. READ MORE
What's Euclid got to do with it?
There's a lot of talk in modular synthesis circles about what people call "Euclidean" rhythms, which are claimed to exist in most kinds of traditional music around the world. Unfortunately, this concept is often oversold, and presented in a way that makes it sound much more complicated than it is. READ MORE
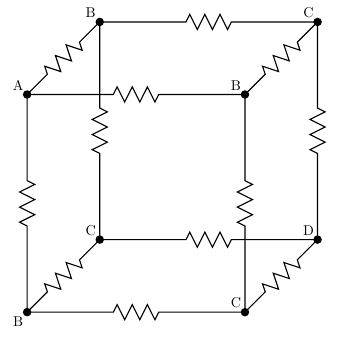
Level up on circuit simplification
In my last entry I talked about the rules for simplifying series and parallel circuits. Two resistors in series can be replaced by one with a value equivalent to the pair of them; two in parallel can similarly be replaced; there are other rules in the same general form for capacitors and inductors (assuming theoretically perfect components); and by applying these rules repeatedly you can simplify complicated circuits down to much simpler equivalents. I also set up an interactive reverse calculator for finding combinations of standard-value components to make up a desired, maybe non-standard, value. READ MORE
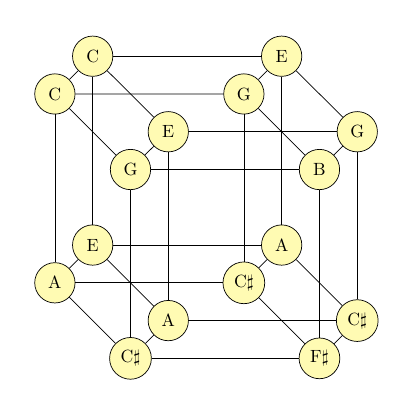
Walking the hypercube
Here is the skeleton of a four-dimensional hypercube, or tesseract, with the vertices labelled by musical note names. READ MORE
Alternate harmony with additive synthesis
Much of musical harmony comes down to combining notes that share harmonics. Sounds produced by (some...) physical objects typically have consistent waveforms, where each wave is the same shape as the last. That is also typical of modular-synth oscillators; and its consequence is that the spectrum always consists of a sum of sine waves all at integer multiples called harmonics of one frequency called the fundamental. The proportions and phases of the different harmonics determine the shape of the waves, and those can vary a lot, but the general pattern of integer multiples is fixed. If you play a note like D with a fundamental frequency of 293.7 Hz, it will have its harmonics at 293.7 Hz, 587.4 Hz, 881.1 Hz, 1174.8 Hz, 1468.5 Hz, 1762.2 Hz, and so on. READ MORE
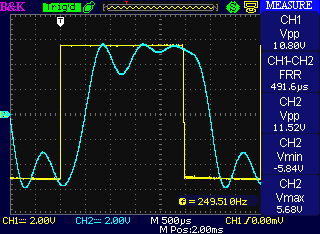
Frequency, latency, and uncertainty
Some wigglers want "fast" envelopes that will turn a signal on and off without any delay and without any perceptible clicking sound. Some wigglers want spectral effects, like frequency shift or vocoding, without any latency between the input and output. Some wigglers just want accurate pitch tracking of external inputs. All of these wigglers are doomed! None of those things can ever work perfectly. But the funny thing is that they're all doomed for the same reason. There is a fundamental principle that limits the performance of all these seemingly different things, and I'll try to explain the connection in this posting without resorting to any particularly complicated math. READ MORE
Live-coding a permutation-based fugue
If you've been following North Coast for a long time, you may remember the live video streams I did back in 2016. This week I spent some time getting the software and hardware set up to do that again, which pretty much meant starting over from scratch because enough things have changed that my former config was no longer appropriate. You can read about the technical side over on my personal site. I'm still not sure exactly how I'll be using this capability, but it's something I've wanted for a long time as a way to raise the profile of some of the stuff I do. In the days to come I'll probably plan out some scheduled broadcasts on music, electronics, and other topics. READ MORE
Listening to the Mandelbrot set
Okay, it's New Year's Eve, I'm overdue to write this week's Web log entry, and the topic I wanted to write about is held up because of (among other things) a package that apparently was stolen from my front porch after it was "delivered" during my vacation and I told them not to mail it so early but blah blah blah... Instead of the exciting mystery topic, let's dig into the back catalog again and think about how to listen to the Mandelbrot set. READ MORE